İstatistik - Lojistik Regresyon

Lojistik regresyon, bir sonucu belirleyen bir veya daha fazla bağımsız değişkenin bulunduğu bir veri setini analiz etmek için istatistiksel bir yöntemdir. Sonuç ikili bir değişkenle ölçülür (burada sadece iki olası sonuç vardır).

Formül

$ {\ pi (x) = \ frac {e ^ {\ alpha + \ beta x}} {1 + e ^ {\ alpha + \ beta x}}} $

Nerede -

Yanıt - Karakteristiğin varlığı / yokluğu.
Öngörücü - Her durum için gözlemlenen sayısal değişken
$ {\ beta = 0 \ Rightarrow} $ P (Varlık), x'in her düzeyinde aynıdır.
$ {\ beta \ gt 0 \ Rightarrow} $ P (Varlık) x arttıkça artar
$ {\ beta = 0 \ Rightarrow} $ P (Varlık) x arttıkça azalır.

Misal

Problem Statement:

Migren için aşağıdaki Rizatriptan probleminin lojistik regresyonunu çözün

Yanıt - Ağrı Tedavisini 2 saatte tamamlayın (Evet / Hayır).

Öngörücü - Doz (mg): Plasebo (0), 2.5,5,10

Doz	# Hastalar	# Kurtarıldı	% Rahatlama
0	67	2	3.0
2.5	75	7	9.3
5	130	29	22.3
10	145	40	27.6

Solution:

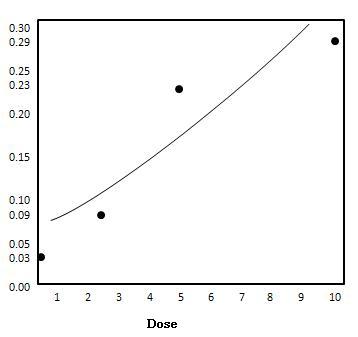
$ {\ Alpha = -2.490} ve $ {\ beta = .165} değerlerine sahip olarak, aşağıdaki verileri elde ediyoruz:

$ {\ pi (0) = \ frac {e ^ {\ alpha + \ beta \ times 0}} {1 + e ^ {\ alpha + \ beta \ times 0}} \\ [7pt] \, = \ frac {e ^ {- 2.490 + 0}} {1 + e ^ {- 2.490}} \\ [7pt] \\ [7pt] \, = 0.03 \\ [7pt] \ pi (2.5) = \ frac {e ^ {\ alpha + \ beta \ times 2.5}} {1 + e ^ {\ alpha + \ beta \ times 2.5}} \\ [7pt] \, = \ frac {e ^ {- 2.490 + .165 \ times 2.5} } {1 + e ^ {- 2.490 + .165 \ times 2.5}} \\ [7pt] \, = 0.09 \\ [7pt] \\ [7pt] \ pi (5) = \ frac {e ^ {\ alpha + \ beta \ times 5}} {1 + e ^ {\ alpha + \ beta \ times 5}} \\ [7pt] \, = \ frac {e ^ {- 2.490 + .165 \ times 5}} {1 + e ^ {- 2.490 + .165 \ times 5}} \\ [7pt] \, = 0.23 \\ [7pt] \\ [7pt] \ pi (10) = \ frac {e ^ {\ alpha + \ beta \ times 10}} {1 + e ^ {\ alpha + \ beta \ times 10}} \\ [7pt] \, = \ frac {e ^ {- 2.490 + .165 \ times 10}} {1 + e ^ {-2.490 + .165 \ times 10}} \\ [7pt] \, = 0.29} $

Doz ($ {x} $)	$ {\ pi (x)} $
0	0.03
2.5	0.09
5	0.23
10	0.29