İstatistik - Artık analizi

Kalıntı analizi, kalıntıları tanımlayarak ve kalıntı grafiklerini inceleyerek doğrusal bir regresyon modelinin uygunluğunu değerlendirmek için kullanılır.

Artık

Artık ($ e $), gözlemlenen değer ($ y $) ile tahmin edilen değer ($ \ hat y $) arasındaki farkı ifade eder. Her veri noktasının bir kalıntısı vardır.

Artık Arsa

Kalıntı grafiği, artıkların dikey eksende ve bağımsız değişkenin yatay eksende olduğu bir grafiktir. Noktalar yatay eksen etrafında rastgele dağılmışsa, veriler için doğrusal bir regresyon modeli uygundur; aksi takdirde doğrusal olmayan bir model seçin.

Kalıntı Arsa Türleri

Aşağıdaki örnek, kalıntı grafiklerdeki birkaç modeli göstermektedir.

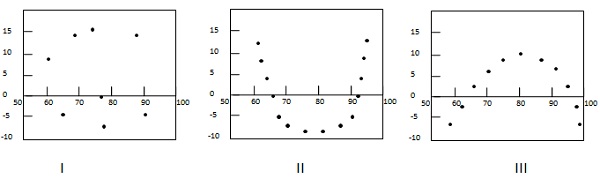
İlk durumda, noktalar rastgele dağılmıştır. Dolayısıyla doğrusal regresyon modeli tercih edilir. İkinci ve üçüncü durumda, noktalar rastgele dağılmamıştır ve doğrusal olmayan bir regresyon yönteminin tercih edildiğini gösterir.

Misal

Problem Statement:

Aşağıdaki veriler için doğrusal bir regresyon modelinin nerede uygun olduğunu kontrol edin.

$ x $	60	70	80	85	95
$ y $ (Gerçek Değer)	70	65	70	95	85
$ \ hat y $ (Öngörülen Değer)	65.411	71.849	78.288	81.507	87.945

Solution:

Step 1: Her veri noktası için artıkları hesaplayın.

$ x $	60	70	80	85	95
$ y $ (Gerçek Değer)	70	65	70	95	85
$ \ hat y $ (Öngörülen Değer)	65.411	71.849	78.288	81.507	87.945
$ e $ (Kalan)	4.589	-6.849	-8.288	13.493	-2.945

Step 2: - Kalan arsa grafiğini çizin.

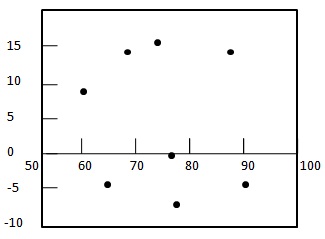
Step 3: - Kalıntıların rastlantısallığını kontrol edin.

Burada kalıntı grafiği rastgele bir model sergiliyor - İlk kalıntı pozitif, sonraki ikisi negatif, dördüncüsü pozitif ve son kalıntı negatif. Model oldukça rastgele olduğundan, bu, doğrusal bir regresyon modelinin yukarıdaki veriler için uygun olduğunu gösterir.