İstatistik - F dağılımı
F dağılımı (Snedecor'un F dağılımı veya Fisher-Snedecor dağılımı), sıklıkla test istatistiklerinin sıfır dağılımı olarak ortaya çıkan sürekli olasılık dağılımını temsil eder. Çoğunlukla varyans analizi veya F testi sırasında olur.
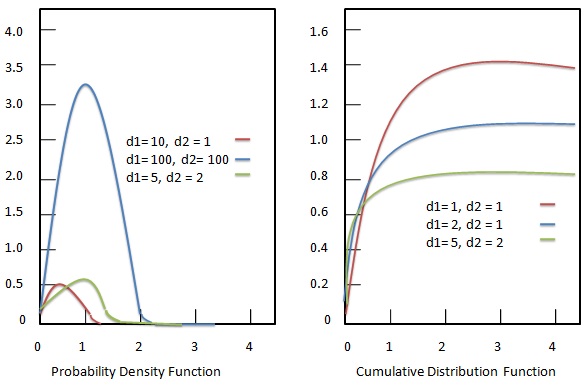
Olasılık yoğunluk işlevi
F dağılımının olasılık yoğunluk fonksiyonu şu şekilde verilir:
Formül
$ {f (x; d_1, d_2) = \ frac {\ sqrt {\ frac {(d_1 x) ^ {d_1} d_2 ^ {d_2}} {(d_1x + d_2) ^ {d_1 + d_2}}}} { x \ beta (\ frac {d_1} {2}, \ frac {d_2} {2})}} $
Nerede -
$ {d_1} $ = pozitif parametre.
$ {d_2} $ = pozitif parametre.
$ {x} $ = rastgele değişken.
Kümülatif dağılım fonksiyonu
F dağılımının kümülatif dağılım işlevi şu şekilde verilir:
Formül
$ {F (x; d_1, d_2) = I _ {\ frac {d_1x} {d_1x + d_2}} (\ frac {d_1} {2}, \ frac {d_2} {2})} $
Nerede -
$ {d_1} $ = pozitif parametre.
$ {d_2} $ = pozitif parametre.
$ {x} $ = rastgele değişken.
$ {I} $ = daha düşük tamamlanmamış beta işlevi.