İstatistikler - Venn Diyagramı
Venn diyagramı, varlık veya nesne grupları arasındaki ilişkiyi görsel olarak temsil etmenin bir yoludur. Venn diyagramları, her dairenin bütün bir seti temsil ettiği dairelerden oluşur. Venn diyagramında sınırsız daire olabilir, ancak genellikle iki veya üç daire tercih edilir, aksi takdirde diyagram çok karmaşık hale gelir.
Venn Şeması çizme adımları
Aşağıdaki insan gruplarını düşünün:
Cricket Players - $ C = \ {Ram, Shyam, Mohan, Rohan, Ramesh, Suresh \} $
Hockey Players - $ H = \ {Ramesh, Naresh, Mahesh, Leela, Sunita \} $
Adım 1: Bir dikdörtgen çizin ve onu oyuncular olarak etiketleyin.
Adım 2: İki daire çizin ve bunları Kriket ve Hokey olarak etiketleyin. Dairelerin birbiriyle örtüştüğünden emin olun.
3. Adım: İsimleri uygun şekilde dairenin içine yazın. Yaygın isimler ortak bölge içinde yer almalıdır.
Birlik
Birleşim ($ \ cup $), öğelerin tüm kategorilerde bulunduğu ancak tekrar edilmediği bir kümeyi temsil eder.
Misal
Problem Statement:
$ C \ cup H $ için bir Venn diyagramı çizin.
Solution:
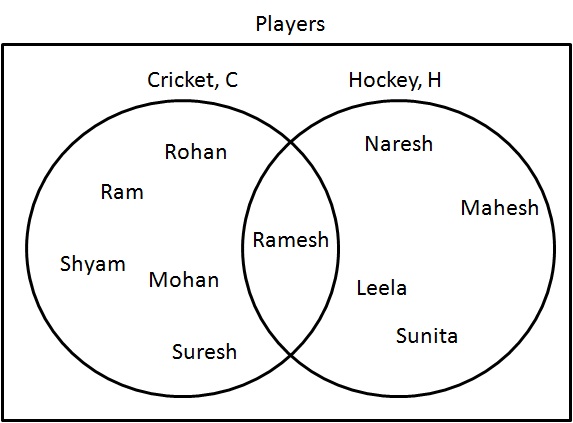
Adım 1: Kriket veya hokey oynayan oyuncuları belirleyin. Bunları aşağıdaki gibi çizin:
$ C \ cup H = \ {Ram, Shyam, Mohan, Rohan, Ramesh, Suresh, Naresh, Mahesh, Leela, Sunita \} $.

Kavşak
Kesişim ($ \ cap $), öğelerin her iki kategoride de mevcut olduğu bir kümeyi temsil eder.
Misal
Problem Statement:
$ C \ cap H $ için bir Venn diyagramı çizin.
Solution:
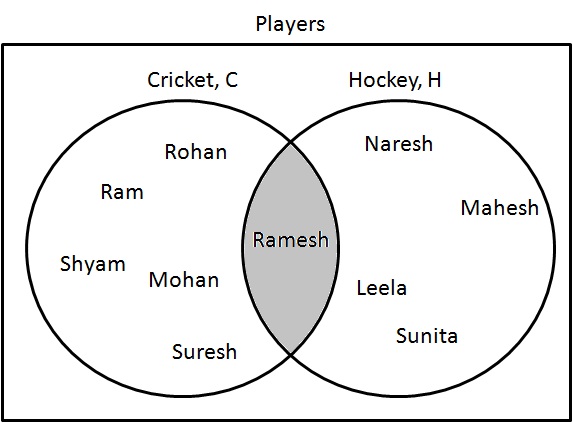
Adım 1: Hem kriket hem de hokey oynayan oyuncuları belirleyin. Bunları aşağıdaki gibi çizin:
$ C \ cap H = \ {Ramesh \} $.
Fark
Fark ($ - $), öğelerin yalnızca bir kategoride mevcut olduğu ve diğerinde bulunmadığı bir kümeyi temsil eder.
Misal
Problem Statement:
$ C - H $ şeklinde bir Venn diyagramı çizin.
Solution:
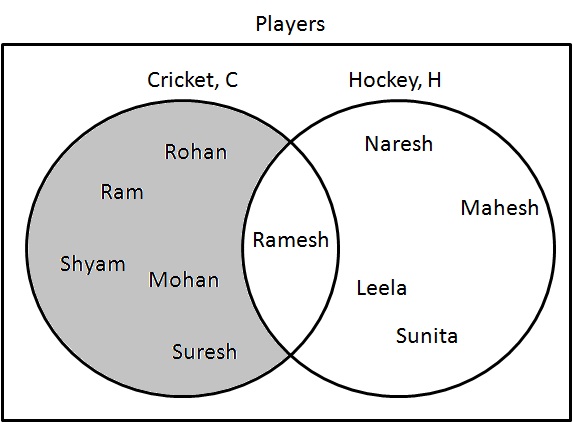
Adım 1: Yalnızca kriket oynayan oyuncuları belirleyin. Bunları aşağıdaki gibi çizin:
$ C - H = \ {Ram, Shyam, Mohan, Rohan, Suresh \} $.