Von der Fermionenphysik

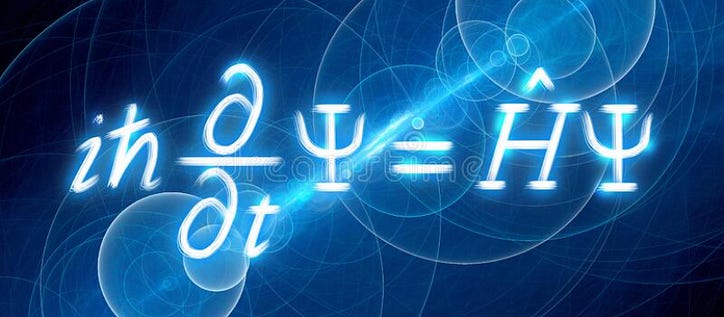
Wenn Sie Quantenphysik studiert haben oder zumindest davon gehört haben, haben Sie vielleicht schon von diesem Schrödinger gehört. Weißt du – der mit der ganzen Katzensache? Nun, er ist auch der Typ hinter einer der nützlichsten Gleichungen in der Quantenmechanik – der Schrödinger-Gleichung. Auf den ersten Blick mag es unmöglich erscheinen, die Gleichung zu lösen (und in einigen Fällen ist sie es tatsächlich!), aber nachdem Sie dies gelesen haben, werden Sie die Gleichung verstehen und sogar, wie Sie sie für ein Szenario lösen können. Bereit? Lass uns gehen.

Hier ist die Gleichung. Es sieht beängstigend aus – es enthält sogar Mistgabeln! Aber lassen Sie uns versuchen, etwas Intuition für diese Gleichung zu gewinnen. Wir werden zunächst über Energie in der Quantenmechanik sprechen, sie zu Operatoren machen und dann über die Rolle der Wellenfunktion sprechen. Danach nähen wir alles zusammen und lösen die Gleichung.

Klassische Mechanik

In der klassischen Mechanik (und Quantenmechanik) lautet die Formel für Energie E = KE + PE, wobei E die Gesamtenergie, KE die kinetische Energie und PE die potentielle Energie ist. Jetzt brauchen KE und PE etwas lange zum Schreiben, also verwenden Physiker die offensichtlichen Symbole von T und V, um kinetische bzw. potentielle Energie darzustellen, um ein paar Millisekunden beim Schreiben zu sparen. Jetzt haben wir also E = T + V

Fußnote: Wenn Sie klassische Mechanik genommen haben, werden Sie vielleicht bemerken, dass wir die Hamiltonsche Formulierung verwenden! Mit der Lagrange-Formulierung beschäftigen wir uns an einem anderen Tag.

Jetzt wissen wir, dass T=p²/2m (Formel für kinetische Energie). Hier ist m = Masse, p = Impuls und das schwierigste Symbol von allen, ½ = halb. Die Masse ist immer konstant, aber der Impuls muss es nicht sein. Wenn jemand eine Kraft auf ein Objekt ausübt, beginnt sich der Impuls zu ändern und weicht von seinem ursprünglichen Wert ab. Was ist nun mit potentieller Energie?

Die Formel für potentielle Energie ist V= -(Integral von F) wobei F die Kraft ist. Es wird deutlich, dass die potentielle Energie von der auf ein Objekt ausgeübten Kraft abhängt. In verschiedenen Szenarien kann Ihre potenzielle Energie unterschiedliche Werte annehmen, da unterschiedliche Kräfte wirken. Zum Beispiel ist das Potential in einem Gravitationsbrunnen V=mgx, aber in einem harmonischen Oszillator wird das Potential V=(1/2)kx². Das ist sehr wichtig, weil sich herausstellt, dass unsere „Szenarien“, in denen wir unsere Schrödinger-Gleichung lösen, wirklich nur unterschiedliche Potenziale sind. Das ergibt später Sinn.

Erste Quantisierung

Jetzt nehmen wir in der Quantenmechanik unsere „Observablen“ (T und E) und lassen sie einen Operator habenGegenstücke. Ein Operator für unsere Zwecke ist nur eine Funktion, die einen Wert aufnimmt und einen anderen ausspuckt. T hat also ein Gegenstück zum kinetischen Energieoperator, normalerweise mit T' bezeichnet, und die Energie nimmt ein Gegenstück zum Energieoperator an, normalerweise mit H bezeichnet. Die potentielle Energie wird „gegeben“ statt gelöst, also hat sie keine Betreiber Gegenstück. Nun ist der kinetische Energieoperator als ein Operator definiert, bei dem er, wenn er auf die Wellenfunktion einwirkt, die kinetische Energie des Teilchens multipliziert mit der Wellenfunktion zurückgibt. Dasselbe gilt für den Energy-Operator. Diese ganze Sache mag ein bisschen nutzlos und abstrakt erscheinen, aber glauben Sie mir, das ist es nicht – wir kommen dorthin. Erinnern Sie sich jetzt, wie T=(1/2m)p²? Dies impliziert, dass T' = (1/2m)p̂², wobei p̂ der Impulsoperator ist . Und wie zuvor gilt p̂ ψ = p ψwobei p der Impuls des Teilchens ist (wieder wirkt ein Operator auf eine Funktion und gibt die Funktion multipliziert mit dem Wert zurück, der mit dem Operator in Beziehung steht). Nun stellt sich heraus, dass der Impulsoperator ist

p̂ = -ih(d/dx). Nimm es erstmal als gegeben hin. Dies impliziert das

T' = -h²/2m (d²/dx²). Und da E = T + V, dann H=(-h²/2m)(d²/dx²) + V. Dann können wir jetzt beide Seiten mit der Wellenfunktion multiplizieren, um zu bekommen

H ψ = -h²/2m (d²ψ/dx²) + Vψ

Und erinnern Sie sich von früher, H ψ = Eψ, also

Eψ = (-h²/2m)(d²ψ/dx²) + Vψ

Atmen Sie jetzt tief durch. Wir haben viel gerechnet und hoffentlich haben Sie sich nicht verlaufen. Es stellt sich heraus, dass wir die Schrödinger-Gleichung gerade „abgeleitet“ haben! Bevor wir nun über die Lösung sprechen, müssen wir darüber sprechen, was diese „Wellenfunktion“ überhaupt ist.

Was ist eine Wellenfunktion?

In der klassischen Mechanik verwenden wir die klassische Hamilton-Gleichung, um die Bewegungsgleichungen für ein Teilchen zu lösen. Die Bewegungsgleichungen sind nur die Gleichungen dafür, wo sich ein Teilchen zu einem bestimmten Zeitpunkt befindet. Beispielsweise lautet die Bewegungsgleichung für ein freies Teilchen x(t)=vt + x0. Wir können die Position des Teilchens für jeden Zeitpunkt finden, wenn wir die Anfangsposition und die Geschwindigkeit haben. In der Quantenmechanik verwenden wir stattdessen die Schrödinger-Gleichung, um etwas zu finden, das als „Wellenfunktion“ bezeichnet wird. Die Wellenfunktion selbst ist physikalisch nicht aussagekräftig – sie bedeutet nichts und sagt Ihnen nichts (direkt). Was aussagekräftig ist, ist das Quadrat der Wellenfunktion, das Ihnen die Wahrscheinlichkeitsdichte gibt. Die Wahrscheinlichkeitsdichte ist nur eine Funktion, die Ihnen die Wahrscheinlichkeit angibt, dass Sie ein Teilchen in einem bestimmten Bereich finden, wenn Sie es messen. Wir können also sagen, dass die Wellenfunktion nur die „Quadratwurzel“ der Wahrscheinlichkeitsdichte ist. Jetzt haben wir endlich das gesamte Hintergrundwissen, um darüber zu sprechen, was die Schrödinger-Gleichung ist .

Wie wir aus der obigen Gleichung ersehen können, ist bis auf die potentielle Energie V(x) alles konstant. Wir nehmen eine bestimmte potentielle Energie und lösen die Gleichung für den Fall, in dem Sie diese bestimmte potentielle Energie haben. Das ist so schön, denn es spielt keine Rolle, welche Belastungen Ihr System hat, oder die Hitze, Ladung, Spannung, was auch immer – Sie müssen nichts davon berücksichtigen . Alles, was Sie wissen müssen, ist nur die potentielle Energiefunktion und Sie können die Gleichung lösen

(Wenn wir hier pedantisch sein wollen, könnten wir sagen, dass wir „technisch“ all diese Dinge in das Potenzial selbst einbeziehen. Außerdem ist das auf dem Kopf stehende Dreieck die Abkürzung für die zweite Ableitung.)

Berechnung

(wenn Sie kein Kalkül mögen, können Sie diesen Teil überspringen)

Lösen wir nun die Schrödinger-Gleichung für ein einfaches Potential, bei dem überall V(x)=0 ist. Dies wird als freies Teilchen bezeichnet, da die Nettokräfte darauf Null sind. Es ist frei von jeglicher Unterdrückung! Im klassischen Fall wäre die Bewegungsgleichung x(t)=vt + x0, was auf einem Raum-Zeit-Graphen eine Gerade bildet. Mal sehen, wie die Wellenfunktion für den Quantenfall aussieht.

Da V(x)=0, dann wird die Schrödinger-Gleichung

-h²/2m(d² ψ/dx²) = Eψ

Wir können dann etwas neu anordnen und bekommen

d² ψ/dx² = -2mEψ/h²

Wir sehen jetzt, dass alle Terme auf der rechten Seite bis auf ψ konstant sind. Das ist gut, weil es die Gleichung einfach zu lösen macht. Wir können dann eine Konstante k als sqrt(2mE/h) definieren, was bedeutet, dass wir jetzt haben

d²ψ / dx² = -k²ψ

Wir addieren dann beide Seiten der Gleichung durch den rechten Term

d²ψ/dx² + k²ψ = 0

Wir nehmen dann an, dass ψ(x) = exp(rx)

und daraus bekommen wir

r=-k², r= +ik oder -ik

Das bedeutet, dass ψ( x)=exp(ikx) bzw

ψ( x)=exp(-ikx)

Da die Gleichung linear ist, können wir eine Überlagerung (Linearkombination) beider Teile nehmen, um die allgemeine Lösung zu erhalten

ψ(x) = Aexp(ikx) + Bexp(-ikx)

und wir sind technisch fertig. Sie fragen sich vielleicht, wie wir überhaupt die Konstanten A und B bestimmen können. Normalerweise würden wir das durch etwas namens Normalisierung tun, aber das ist eine andere Geschichte. Es stellt sich heraus, dass für dieses Szenario nicht normalisiert werden kann. Das ist eine ausgefallene Sprache, denn die Wellenfunktion nähert sich nicht Null, wenn Sie ins Unendliche oder minus Unendliche gehen. Welche A- und B-Werte entsprechen also diesem Zustand? Nun, es stellt sich heraus, dass dies eigentlich kein möglicher Zustand ist, da Sie ihn nicht normalisieren können. Hoppla!

Aber keine Sorge! Es stellt sich heraus, dass eine Überlagerung aller möglichen Wellenfunktionen einen realen Zustand ergeben kann. Das bringt viele coole Dinge mit sich – aber auch das ist eine Geschichte für das nächste Mal.

Danke fürs Lesen! Diese Website macht einen schrecklichen Job bei der Formatierung mathematischer Symbole, daher wurde ein Teil des mathematischen Textes nicht gut angezeigt. Wenn Sie eine Videoableitung derselben Sache sehen möchten, habe ich hier auf meinem Kanal Fermion Physics ein Video über die Lösung gemacht (obwohl ich ziemlich schnell spreche). Wechseln Sie zwischen dem Video und diesem Artikel, um die Lösung klarer zu machen. Bis zum nächsten Mal!