आसानी से डिग्री को रेडियन में कैसे बदलें (और रेडियन को डिग्री में)

एनबीए कोच और पूर्व खिलाड़ी जेसन किड के लिए एक कुख्यात उद्धरण है: "हम इस टीम को 360 डिग्री के आसपास मोड़ने जा रहे हैं!"

ओह। गणित के शिक्षकों की नजर उस पर पड़ी होगी।

जैसा कि आप पहले से ही जानते होंगे कि एक वृत्त बिल्कुल 360 डिग्री से बना होता है। अगर किड ने अपने वादे को पूरा किया होता, तो उनकी टीम ठीक हो जाती। परेशानी यह है कि, दस्ते तब तक मुड़ना बंद नहीं करेगा जब तक कि वह "पूर्ण चक्र में नहीं चला गया" और ठीक उसी स्थान पर समाप्त हो गया जहां उसने शुरू किया था।

सुधार का नुस्खा नहीं है। किड अपनी टीम को 180 डिग्री के आसपास घुमाने और उन्हें विजेता बनाने की तलाश में था!

डिग्री, परिभाषित

इस संदर्भ में डिग्री एक इकाई है जिसका उपयोग हम कोणों को मापने के लिए कर सकते हैं । कागज पर, डिग्री को डिग्री प्रतीक द्वारा दर्शाया जाता है, जो इस तरह दिखता है: °

इसलिए " 18 डिग्री " लिखने के बजाय आप बस " 18 डिग्री " लिख सकते हैं ।

त्रिकोणमिति और ज्यामिति में सबसे महत्वपूर्ण अवधारणाओं में से एक समकोण है । यह वह कोण है जो बनता है जहाँ दो लंबवत रेखाएँ प्रतिच्छेद करती हैं।

यह एक पूर्ण रोटेशन के एक चौथाई का भी प्रतिनिधित्व करता है।

मान लीजिए कि आप शारीरिक रूप से कुछ मोड़ना चाहते हैं। कुछ भी। आपने एक निश्चित केंद्र बिंदु चुना है और उस वस्तु को उसके चारों ओर एक गोलाकार गति में घुमाने की कोशिश कर रहे हैं। यदि आप कार्य पूरा करते हैं और एक पूर्ण चक्र बनाते हैं, तो यह एक पूर्ण घूर्णन है। लेकिन अगर आप प्रक्रिया को 25 प्रतिशत रास्ते से रोक देते हैं, तो यह पूर्ण रोटेशन का केवल एक चौथाई हिस्सा है। जो आपको एक समकोण देता है।

एक समकोण 90 डिग्री (यानी 360 का 25 प्रतिशत) के बराबर होता है। इसे लगाने का एक और तरीका यहां दिया गया है : एक समकोण π/2 रेडियन के बराबर होता है ।

समय समाप्त! एक रेडियन क्या है? और इसमें ( पाई ) कैसे मिश्रित हो गया?

रेडियन खोलना

ठीक है, एक पूर्ण चक्र की कल्पना करें। एक सीधी रेखा है जो अपने सटीक केंद्र से शुरू होती है और सर्कल के घुमावदार परिधि (जैसे बाहरी किनारे) पर समाप्त होती है।

परिभाषा के अनुसार, वह रेखा हमारे वृत्त की त्रिज्या है।

मूलतः, एक रेडियन एक वृत्त का एक टुकड़ा है। वृत्त की घुमावदार बाहरी परिधि को एक बार और देखें। अब परिधि के एक खंड की कल्पना करें जो आपके वृत्त की त्रिज्या की लंबाई के बराबर हो। यदि आप दो सीधी रेखाएँ खींचते हैं जो इसके दो समापन बिंदुओं को वृत्त के सटीक केंद्र से जोड़ते हैं, तो वे जो कोण उत्पन्न करेंगे वह एक रेडियन होगा।

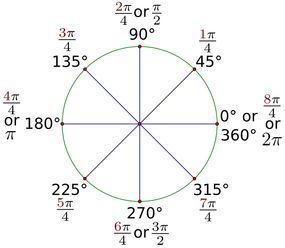
प्रत्येक सर्कल में समान संख्या में रेडियंस के लिए जगह होती है। वह संख्या 2 गुना pi ("π") के बराबर है। चूँकि pi स्वयं लगभग 3.14 के बराबर है, आप कह सकते हैं कि एक वृत्त (2 x 3.14) में लगभग 6.28 रेडियन हैं। या कि 1 रेडियन लगभग 57.29 डिग्री (180°/π) है।

रेडियन बनाम। डिग्री

देखिए, हम इनकार नहीं करेंगे। डिग्री की तुलना में रेडियन की कल्पना करना एक कठिन अवधारणा हो सकती है।

लेकिन पूर्व छूट मत करो। इन दोनों कोण-मापने वाली इकाइयों के अपने फायदे हैं।

डिग्री ज्यादा लोकप्रिय है। वास्तविक दुनिया में, आप ऐसे लोगों से मिलने की अधिक संभावना रखते हैं जो रेडियन के विपरीत डिग्री के संदर्भ में सोचते हैं। इसलिए, यदि आप एक गैर-गणितज्ञ के साथ संवाद करने की कोशिश कर रहे हैं, तो शायद डिग्री से चिपके रहें।

हालांकि, कैलकुलस में, रेडियन महान होते हैं क्योंकि वे खुद को बहुत सरल समीकरणों के लिए उधार देते हैं । भविष्य के एपी छात्र इसे ध्यान में रखना चाहेंगे।

डिग्री को रेडियन में बदलना (और इसके विपरीत)

डिग्री को रेडियन में बदलने के लिए, आपको बस कुछ आसान चरणों को याद रखना होगा।

सबसे पहले, उन डिग्रियों की संख्या लें जिन्हें आप कनवर्ट करना चाहते हैं। इस संख्या को रेडियन/180 डिग्री से गुणा करें । कुछ अनावश्यक इकाइयों को हटाकर और फिर चीजों को थोड़ा सरल करके, आपके पास अपना उत्तर होगा।

मान लीजिए कि आपके पास एक धातु की पट्टी है जो 120 डिग्री के कोण पर मुड़ी हुई है। इसे हम रेडियन के रूप में कैसे व्यक्त कर सकते हैं?

यह पता लगाने के लिए, हम अपना समीकरण इस प्रकार लिखेंगे:

120 ° x (π रेडियन/180 ° )

ऊपर दिखाए गए डिग्री प्रतीकों की जोड़ी पर ध्यान दें। वे एक दूसरे को रद्द कर देंगे, यह सुनिश्चित करते हुए कि हमारा अंतिम उत्तर रेडियन में होगा। अब हमारे पास बचा है:

120 x (π रेडियन/180)

गुणा करें और आपको 120π/180 रेडियन मिलते हैं । लेकिन हम अभी पूरी तरह से तैयार नहीं हैं। अब यदि संभव हो तो हमें अपने भिन्न को सरल बनाना होगा। हमें उस उच्चतम पूर्ण संख्या की पहचान करने की आवश्यकता है जिसे हर (180) और अंश के गैर-π भाग (120) दोनों में पूर्ण रूप से विभाजित किया जा सकता है। स्पॉयलर अलर्ट: हमारे मामले में, जादुई संख्या 60 है।

यदि आप वास्तव में 120π और 180 को 60 से विभाजित करते हैं, तो आपको 2π/3 रेडियन मिलते हैं।

तो, हम वहां जाते हैं: 120° 2π/3 रेडियन के बराबर है।

रेडियन से डिग्री तक जाना एक समान प्रक्रिया है । केवल इस मामले में, हम रेडियन की प्रारंभिक मात्रा लेंगे और इसे (180 ° / π ) से गुणा करेंगे।

π/3 रेडियन x (180 ° / π) = 60 डिग्री

संक्षेप में:

रेडियन से डिग्री में बदलने के लिए : 180 से गुणा करें, . से भाग दें

डिग्री से रेडियन में बदलने के लिए : π से गुणा करें, 180 . से भाग दें

अब यह दिलचस्प है

एक ही केंद्र को साझा करने वाले दो संकेंद्रित वृत्तों से बनी "रिंग" आकृति को तकनीकी रूप से " एनलस " कहा जाता है ।