フェルミオン物理学による

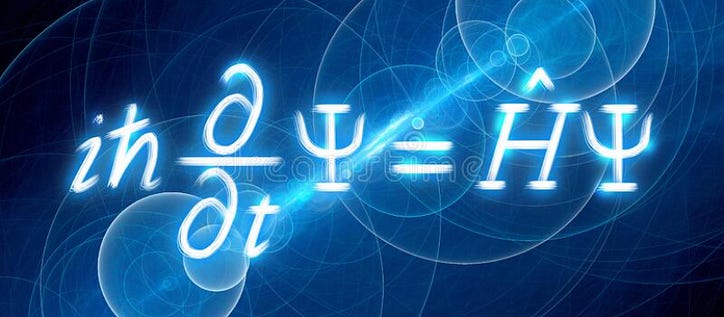
量子物理学を学んだことがある、または少なくともそれについて聞いたことがある場合は、このシュレーディンガーの男のことを聞いたことがあるかもしれません. ご存知のように、猫全体のものですか？彼はまた、量子力学で最も有用な方程式の 1 つであるシュレディンガー方程式の背後にいる人物でもあります。一見すると、この方程式を解くことは不可能に思えるかもしれません (実際、場合によってはそうです!)。しかし、これを読めば、方程式と、1 つのシナリオでそれを解く方法さえも理解できるようになります。準備？行こう。

これが方程式です。恐ろしく見えます - 熊手まで入っています。しかし、この方程式についていくつかの直感を得ようとしましょう。最初に量子力学のエネルギーについて話し、それらを演算子に昇格させ、次に波動関数の役割について話します。その後、すべてをつなぎ合わせて方程式を解きます。

古典力学

古典力学 (および量子力学) では、エネルギーの公式は E = KE + PE です。ここで、Eは全エネルギー、KEは運動エネルギー、PE はポテンシャル エネルギーです。現在、KE と PE の書き込みには少し時間がかかるため、数ミリ秒の書き込み時間を節約するために、物理学者は T と V の明白な記号を使用して、それぞれ運動エネルギーと位置エネルギーを表しています。これで、E = T + V が得られました。

脚注: 古典力学を学んだことがあれば、ハミルトン定式化を使用していることに気付くかもしれません! ラグランジュ定式化については別の日に扱います。

これで、T=p²/2m (運動エネルギーの式) がわかりました。ここで、m = 質量、p = 運動量、そしてすべての中で最も難しい記号である ½ = 半分です。質量は常に一定ですが、運動量は一定である必要はありません。誰かが物体に力を加えると、運動量が変化し始め、元の値から逸脱します。では、位置エネルギーはどうでしょうか。

ポテンシャル エネルギーの式は V= -(F の積分) で、F は力です。位置エネルギーは、物体にかかる力に依存することが明らかになります。さまざまなシナリオでは、さまざまな力が存在するため、位置エネルギーはさまざまな値をとる可能性があります。たとえば、重力井戸ではポテンシャルは V=mgx ですが、調和振動子ではポテンシャルは V=(1/2)kx² になります。シュレディンガー方程式を解くための「シナリオ」は、実際にはさまざまな可能性であることが判明したため、これは非常に重要です。これは後で意味が分かります。

最初の量子化

量子力学では、「観測量」(T と E) を取り、それらに演算子を持たせます。カウンターパート。ここでの演算子は、ある値を取り込んで別の値を吐き出す単なる関数です。したがって、T には通常 T' で示される運動エネルギー演算子の対応物があり、エネルギーは通常 H で示されるエネルギー演算子の対応物を取ります。ポテンシャル エネルギーは解かれるのではなく「与えられる」ので、オペレーター相手。ここで、運動エネルギー演算子は、波動関数に作用するときに、粒子の運動エネルギーに波動関数を掛けた値を返す演算子として定義されます。Energy オペレーターと同じことです。この全体は少し役に立たず抽象的に見えるかもしれませんが、そうではないと信じてください - 私たちはそこに到達しています. T=(1/2m)p² を覚えていますか? これは、T' = (1/2m)p^² を意味します。ここで、p^ は運動量演算子です。前と同じように、 p̂ ψ = p ψここで、p は粒子の運動量です (ここでも、演算子は関数に作用し、演算子に関連する値を乗算した関数を返します)。これで、運動量演算子は

p^ = -ih(d/dx)。とりあえず当たり前と思ってください。これは、

T' = -h²/2m (d²/dx²)。E = T + V なので、H=(-h²/2m)(d²/dx²) + V. 次に、波動関数を両辺に掛けて、

H ψ = -h²/2m (d²ψ/dx²) + Vψ

先ほどのことを思い出してください、H ψ = Eψ ですから、

E ψ = (-h²/2m)(d²ψ/dx²) + Vψ

今、深呼吸してください。私たちは多くの計算を行いましたが、あなたが迷子にならないことを願っています. シュレディンガー方程式を「導出」したことがわかりました。それを解くことについて話す前に、この「波動関数」とは何かについて話す必要があります。

波動関数とは？

古典力学では、古典的なハミルトニアン方程式を使用して、粒子の運動方程式を解きます。運動方程式は、粒子が特定の瞬間にどこにあるかを表す方程式にすぎません。たとえば、自由粒子の運動方程式は x(t)=vt + x0 です。初期位置と速度があれば、任意の瞬間の粒子の位置を見つけることができます。量子力学では、代わりにシュレディンガー方程式を使用して、「波動関数」と呼ばれるものを見つけます。波動関数自体は物理的に意味がありません — それは何の意味もありませんし、(直接的に) 何も教えてくれません。意味があるのは、確率密度を与える波動関数の 2 乗です。. 確率密度は、測定したときにある範囲内に粒子が見つかる可能性を示す単なる関数です。したがって、波動関数は確率密度の「平方根」であると言えます。これで、シュレディンガー方程式とは何かについて説明するための背景知識がすべて揃いました。

上記の式からわかるように、ポテンシャル エネルギー V(x) を除いて、すべてが一定です。特定のポテンシャル エネルギーを取り、その特定のポテンシャル エネルギーがある場合の方程式を解きます。これは非常に素晴らしいことです。なぜなら、システムにどんなストレスがかかっていても、熱、電荷、電圧など、名前を付ける必要がないからです。あなたが知る必要があるのは、ポテンシャルエネルギー関数だけで、方程式を解くことができます

(ここで衒学的になりたい場合は、「技術的に」、これらすべてのものをポテンシャル自体の中に組み込んでいると言えます。また、逆三角形のものは 2 次導関数の略です)

計算

（微積分が苦手な方は飛ばしてください）

ここで、どこでも V(x)=0 である単純なポテンシャルのシュレディンガー方程式を解いてみましょう。これは、正味の力がゼロであるため、自由粒子として知られています。それはすべての抑圧から解放されています！古典的なケースでは、運動方程式は x(t)=vt + x0 となり、時空グラフ上で直線を形成します。量子の場合の波動関数がどのように見えるか見てみましょう。

V(x)=0 なので、シュレディンガー方程式は次のようになります。

-h²/2m(d² ψ/dx²) = Eψ

次に、いくつかの再配置を行い、取得できます

d² ψ/dx² = -2mEψ/h²

ここで、右辺のすべての項がψ を除いて一定であることがわかります。これ は、方程式を簡単に解くことができるため、優れています。次に、定数 k を sqrt(2mE/h) と定義できます。つまり、次のようになります。

d²ψ / dx² = -k²ψ

次に、式の両辺を右辺の項で加算します

d²ψ/dx² + k²ψ = 0

次に、 ψ(x) = exp(rx)と仮定します。

そしてこれから得ます

r=-k²、r= +ik または -ik

これは、ψ( x)=exp(ikx) または

ψ( x)=exp(-ikx)

方程式は線形であるため、両方の部分の重ね合わせ (線形結合) をとって一般解を得ることができます。

ψ(x) = Aexp(ikx) + Bexp(-ikx)

技術的には完了です。定数 A と B をどのように決定できるのか疑問に思われるかもしれません。通常はこれを正規化と呼ばれる方法で行いますが、それはまた別の機会にします。このシナリオでは正規化できないことがわかりました。これは、波動関数が無限大またはマイナス無限大に行くときにゼロに近づかないための派手な言語です。では、この状態に対応する A 値と B 値は何ですか? 正規化できないため、これは実際には可能な状態ではないことがわかりました。おっとっと！

でも心配はいりません！考えられるすべての波動関数の重ね合わせによって、実際の状態が得られることがわかりました。これはそれ自体で多くの優れた機能をもたらしますが、それもまた次回の話です。

読んでくれてありがとう！この Web サイトでは、数学記号の書式設定がひどいため、一部の数学テキストがうまく表示されませんでした。同じことのビデオ派生を見たい場合は、私のチャンネルFermion Physics でこのソリューションに関するビデオを作成しました (ただし、非常に速く話します)。ビデオとこの記事を切り替えると、解決策がより明確になります。次回まで！