Fermiyon Fiziği tarafından

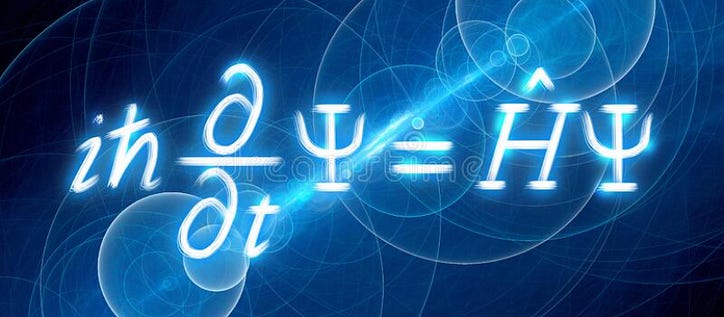
Kuantum fiziğini aldıysanız veya en azından duyduysanız, bu Schrödinger denen herifi duymuş olabilirsiniz. Bilirsin - tüm kedi olayı olan? Aynı zamanda kuantum mekaniğindeki en yararlı denklemlerden birinin arkasındaki adamdır - Schrödinger denklemi. İlk bakışta, denklemi çözmek imkansız görünebilir (ve aslında bazı durumlarda öyle!), ancak bunu okuduktan sonra denklemi ve hatta bir senaryo için nasıl çözeceğinizi anlayacaksınız. Hazır? Hadi gidelim.

İşte denklem. Korkunç görünüyor - içinde dirgenler bile var! Ama bu denklem hakkında biraz sezgi kazanmaya çalışalım. İlk önce kuantum mekaniğinde enerjiden bahsederek başlayacağız, bunları operatörlere tanıtacağız, ardından dalga fonksiyonunun rolü hakkında konuşacağız. Bundan sonra, her şeyi birbirine dikeceğiz ve denklemi çözeceğiz.

Klasik mekanik

Klasik mekanikte (ve kuantum mekaniğinde), enerji formülü E = KE + PE'dir; burada E toplam enerji, KE kinetik enerji ve PE potansiyel enerjidir. Şimdi KE ve PE'nin yazılması biraz uzun sürüyor, bu nedenle birkaç milisaniye yazmaktan tasarruf etmek için fizikçiler sırasıyla kinetik ve potansiyel enerjiyi temsil etmek için T ve V'nin bariz sembollerini kullanıyorlar. Şimdi elimizde E = T + V var

Dipnot: Klasik mekaniği aldıysanız, Hamiltonian formülasyonunu kullandığımızı fark edebilirsiniz! Lagrangian formülasyonunu başka bir gün ele alırız.

Artık T=p²/2m (kinetik enerji formülü) olduğunu biliyoruz. Burada m=kütle, p=momentum ve en sert sembol ½=yarı. Kütle her zaman sabittir, ancak momentum sabit olmak zorunda değildir. Birisi bir nesneye kuvvet uygularsa, momentum değişmeye başlayacak ve orijinal değerinden sapacaktır. Peki ya Potansiyel enerji?

Potansiyel enerjinin formülü, F'nin kuvvet olduğu V= -(F'nin integrali) şeklindedir. Görüldüğü gibi potansiyel enerji bir cisme uygulanan kuvvete bağlıdır. Farklı senaryolarda, farklı kuvvetler olduğu için potansiyel enerjiniz farklı değerler alabilir. Örneğin yerçekimi kuyusunda potansiyel V=mgx iken harmonik osilatörde potansiyel V=(1/2)kx² olur. Bu çok önemli, çünkü Schrödinger denklemimizi çözdüğümüz "senaryolarımız"ın gerçekten farklı potansiyeller olduğu ortaya çıktı. Bu daha sonra mantıklı olacaktır.

İlk Kuantizasyon

Şimdi kuantum mekaniğinde, "gözlemlenebilirlerimizi" (T ve E) alıyoruz ve onların operatöre sahip olmasını sağlıyoruz.muadilleri Amaçlarımız açısından bir operatör, yalnızca bir değeri alan ve diğerini veren bir işlevdir. Dolayısıyla T'nin, genellikle T' ile gösterilen bir kinetik enerji operatörü karşılığı vardır ve enerji, genellikle H ile gösterilen bir enerji operatörü karşılığı alır. Potansiyel enerji, çözülmek yerine "verilir", bu nedenle herhangi operatör muadili Şimdi kinetik enerji operatörü, dalga fonksiyonu üzerinde etkide bulunduğunda parçacığın kinetik enerjisini dalga fonksiyonu ile çarparak döndüren bir operatör olarak tanımlanır. Enerji operatörü ile aynı şey. Bütün bunlar biraz yararsız ve soyut görünebilir, ama güven bana öyle değil - oraya gidiyoruz. Şimdi T=(1/2m)p²'nin nasıl olduğunu hatırlıyor musunuz? Bu, T' = (1/2m)p̂² anlamına gelir, burada p̂ momentum operatörüdür. Ve daha önce olduğu gibi, p̂ ψ = p ψburada p, parçacığın momentumudur (yine, bir operatör bir fonksiyona etki eder ve fonksiyonu, operatörle ilgili değer ne olursa olsun çarpımıyla döndürür). Şimdi momentum operatörünün olduğu ortaya çıktı.

p̂ = -ih(d/dx). Şimdilik verili olarak kabul edin. Bu şu anlama gelir

T' = -h²/2m (d²/dx²). Ve E = T + V olduğundan, H=(-h²/2m)(d²/dx²) + V. O zaman şimdi her iki tarafı da dalga fonksiyonuyla çarpabiliriz.

H ψ = -h²/2m (d²ψ/dx²) + Vψ

Ve daha önce hatırlayın, H ψ = Eψ, yani

E ψ = (-h²/2m)(d²ψ/dx²) + Vψ

Şimdi derin bir nefes alın. Çok fazla matematik yaptık ve umarım kaybolmamışsınızdır. Görünüşe göre Schrödinger denklemini az önce "türettik"! Şimdi onu çözmekten bahsetmeden önce, bu "dalga fonksiyonunun" ne olduğundan bahsetmemiz gerekiyor.

Dalga fonksiyonu nedir?

Klasik mekanikte, bir parçacığın hareket denklemlerini çözmek için klasik hamilton denklemini kullanırız. Hareket denklemleri, sadece bir parçacığın zamanın belirli bir anında nerede olduğunu gösteren denklemlerdir. Örneğin, serbest bir parçacığın hareket denklemi x(t)=vt + x0'dır. İlk konumumuz ve hızımız varsa, parçacığın herhangi bir andaki konumunu bulabiliriz. Kuantum mekaniğinde bunun yerine "dalga fonksiyonu" denen bir şeyi bulmak için Schrödinger denklemini kullanırız. Dalga fonksiyonunun kendisi fiziksel olarak anlamlı değildir - hiçbir şey ifade etmez ve size (doğrudan) hiçbir şey söylemez. Anlamlı olan , size olasılık yoğunluğunu veren dalga fonksiyonunun karesidir.. Olasılık yoğunluğu, bir parçacığı ölçtüğünüzde belirli bir aralıkta bulma şansınızı söyleyen bir fonksiyondur. Böylece dalga fonksiyonunun olasılık yoğunluğunun sadece "karekökü" olduğunu söyleyebiliriz. Şimdi nihayet Schrödinger denkleminin ne olduğu hakkında konuşmak için tüm arka plan bilgisine sahibiz .

Yukarıdaki denklemden de görebileceğimiz gibi, potansiyel enerji V(x) dışında her şey sabittir. Belirli bir potansiyel enerjiyi alıyoruz ve bu belirli potansiyel enerjiye sahip olduğunuz durum için denklemi çözüyoruz. Bu çok güzel, çünkü sisteminizde ne tür baskılar olduğu veya ısı, yük, voltaj, adını siz koyun, bunların hiçbirini hesaba katmanız gerekmiyor . Bilmeniz gereken tek şey potansiyel enerji fonksiyonudur ve denklemi çözebilirsiniz.

(Burada bilgiçlik yapmak istiyorsak, "teknik olarak" tüm bunları potansiyelin içine dahil ettiğimizi söyleyebiliriz. Ayrıca ters üçgen, ikinci türevin kısaltmasıdır)

Hesaplama

(Matematikten hoşlanmıyorsanız bu kısmı atlayabilirsiniz)

Şimdi, her yerde V(x)=0 olan basit bir potansiyel için Schrödinger denklemini çözelim. Bu, üzerindeki net kuvvetler sıfır olduğu için serbest parçacık olarak bilinir. Tüm baskılardan arınmış! Klasik durumda, uzay-zaman grafiğinde düz bir çizgi oluşturan hareket denklemi x(t)=vt + x0 olacaktır. Kuantum durumu için dalga fonksiyonunun nasıl göründüğüne bakalım.

V(x)=0 olduğundan, schrodinger denklemi şöyle olur:

-h²/2m(d² ψ/dx²) = Eψ

Daha sonra biraz yeniden düzenleme yapabilir ve

d² ψ/dx² = -2mEψ/h²

Şimdi sağ taraftaki tüm terimlerin ψ hariç sabit olduğunu görebiliriz. Bu iyidir çünkü denklemin çözülmesini kolaylaştırır. Daha sonra bir k sabitini sqrt(2mE/h) olarak tanımlayabiliriz, bu da artık sahip olduğumuz anlamına gelir.

d²ψ / dx² = -k²ψ

Daha sonra denklemin her iki tarafını da sağ taraftaki terimle toplarız.

d²ψ/dx² + k²ψ = 0

O zaman ψ(x) = exp(rx) olduğunu varsayarız.

ve bundan şunu elde ederiz

r=-k², r= +ik veya -ik

Bu, ψ( x)=exp(ikx) veya

ψ( x)=exp(-ikx)

Denklem doğrusal olduğundan , genel çözümü elde etmek için her iki parçanın üst üste binmesini (doğrusal kombinasyon) alabiliriz.

ψ(x) = Aexp(ikx) + Bexp(-ikx)

ve teknik olarak işimiz bitti. A ve B sabitlerini bile nasıl belirleyebileceğimizi merak ediyor olabilirsiniz. Bunu genellikle normalleştirme denen bir şeyle yapardık, ama bu başka bir zamanın hikayesi. Bu senaryo için normalleştirilemeyeceği ortaya çıktı. Sonsuza veya eksi sonsuza giderken dalga fonksiyonunun sıfıra yaklaşmaması için süslü bir dil. Peki hangi A ve B değerleri bu duruma karşılık gelir? Normalleştiremeyeceğiniz için bunun aslında olası bir durum olmadığı ortaya çıktı. Hata!

Endişelenme! Tüm olası dalga fonksiyonlarının üst üste bindirilmesinin gerçek bir durum sağlayabileceği ortaya çıktı. Bu, kendine ait pek çok harika şey getiriyor - ama bu da bir sonraki sefer için bir hikaye.

Okuduğunuz için teşekkürler! Bu web sitesi, matematiksel sembolleri biçimlendirmede berbat bir iş çıkarıyor, bu nedenle matematik metninin bir kısmı iyi görünmüyordu. Aynı şeyin bir video türevini görmek isterseniz, burada kanalım Fermion Physics'te çözüm hakkında bir video yaptım (yine de oldukça hızlı konuşuyorum). Video ile bu makale arasında geçiş yapmak, çözümü daha net hale getirmeye yardımcı olacaktır. Bir dahaki sefere kadar!