Oleh Fisika Fermion

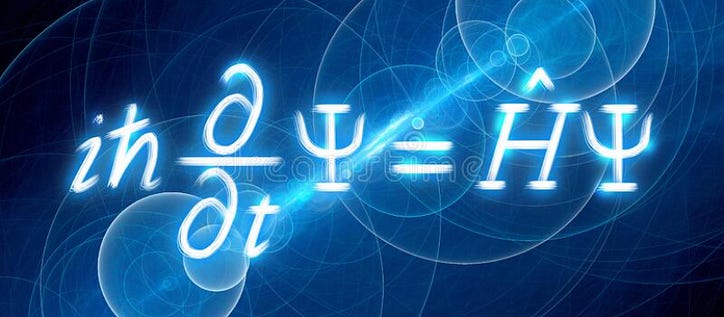
Jika Anda pernah mempelajari fisika kuantum, atau setidaknya pernah mendengarnya, Anda mungkin pernah mendengar tentang orang Schrodinger ini. Anda tahu - yang memiliki masalah kucing? Nah, dia juga orang di balik salah satu persamaan paling berguna dalam mekanika kuantum — persamaan Schrodinger. Pada pandangan pertama, persamaan tersebut mungkin tampak mustahil untuk dipecahkan (dan memang dalam beberapa kasus, memang demikian!), tetapi setelah membaca ini, Anda akan memahami persamaan tersebut dan bahkan cara menyelesaikannya untuk satu skenario. Siap? Ayo pergi.

Berikut persamaannya. Tampaknya menakutkan - bahkan ada garpu rumput di dalamnya! Tapi mari kita coba mendapatkan intuisi tentang persamaan ini. Pertama-tama kita akan mulai dengan berbicara tentang energi dalam mekanika kuantum, mempromosikannya ke operator, lalu berbicara tentang peran fungsi gelombang. Setelah itu, kita akan menggabungkan semuanya dan menyelesaikan persamaannya.

Mekanika Klasik

Dalam mekanika klasik (dan mekanika kuantum), rumus energi adalah E = KE + PE dimana E adalah energi total, KE adalah energi kinetik, dan PE adalah energi potensial. Sekarang KE dan PE membutuhkan waktu agak lama untuk menulis, jadi untuk menghemat beberapa milidetik penulisan, fisikawan menggunakan simbol T dan V yang jelas untuk masing-masing mewakili energi kinetik dan potensial. Jadi sekarang kita memiliki E = T + V

Catatan Kaki: Jika Anda mempelajari mekanika klasik, Anda mungkin memperhatikan bahwa kami menggunakan formulasi Hamiltonian! Kami akan membahas formulasi Lagrangian di lain hari.

Sekarang kita tahu bahwa T=p²/2m (rumus energi kinetik). Di sini, m=massa, p=momentum, dan simbol yang paling sulit, ½=setengah. Massa selalu konstan, tetapi momentum tidak harus demikian. Jika seseorang memberikan gaya pada suatu benda, momentumnya akan mulai berubah dan menyimpang dari nilai awalnya. Sekarang bagaimana dengan energi Potensial?

Rumus energi potensial adalah V= -(integral dari F) di mana F adalah gaya. Jelaslah bahwa energi potensial bergantung pada gaya yang diterapkan pada suatu benda. Dalam skenario yang berbeda, energi potensial Anda dapat mengambil nilai yang berbeda karena ada gaya yang berbeda. Misalnya, dalam sumur gravitasi, potensialnya adalah V=mgx, tetapi dalam osilator harmonik, potensialnya menjadi V=(1/2)kx². Ini sangat penting karena ternyata “skenario” tempat kita menyelesaikan persamaan Schrodinger sebenarnya hanyalah potensi yang berbeda. Ini akan masuk akal nanti.

Kuantisasi Pertama

Sekarang dalam mekanika kuantum, kami mengambil "observables" kami (T dan E) dan membuatnya memiliki operatorrekan. Operator untuk tujuan kita hanyalah sebuah fungsi yang mengambil satu nilai dan mengeluarkan nilai lainnya. Jadi T memiliki mitra operator energi kinetik, biasanya dilambangkan dengan T', dan energi mengambil mitra operator energi, biasanya dilambangkan dengan H. Energi potensial “diberikan” bukan dipecahkan, sehingga tidak memiliki mitra operator. Sekarang operator energi kinetik didefinisikan sebagai operator dimana ketika bekerja pada fungsi gelombang, ia mengembalikan energi kinetik partikel dikalikan dengan fungsi gelombang. Hal yang sama dengan operator Energi. Semua ini mungkin tampak sedikit tidak berguna dan abstrak, tapi percayalah tidak - kita sedang menuju ke sana. Sekarang ingat bagaimana T=(1/2m)p²? Ini menyiratkan bahwa T' = (1/2m)p̂², di mana p̂ adalah operator momentum . Dan seperti sebelumnya, p̂ ψ = p ψdi mana p adalah momentum partikel (sekali lagi, operator bekerja pada suatu fungsi dan mengembalikan fungsi yang dikalikan dengan nilai apa pun yang terkait dengan operator). Sekarang ternyata operator momentumnya

p̂ = -ih(d/dx). Anggap saja sebagai hadiah untuk saat ini. Ini menyiratkan bahwa

T' = -h²/2m (d²/dx²). Dan karena E = T + V, maka H=(-h²/2m)(d²/dx²) + V. Sekarang kita dapat mengalikan kedua sisi dengan fungsi gelombang untuk mendapatkan

H ψ = -h²/2m (d²ψ/dx²) + Vψ

Dan ingat sebelumnya, H ψ = Eψ, jadi

E ψ = (-h²/2m)(d²ψ/dx²) + Vψ

Sekarang ambil napas dalam-dalam. Kami melakukan banyak perhitungan dan mudah-mudahan Anda tidak tersesat. Ternyata kita baru saja "menurunkan" persamaan Schrodinger! Sekarang sebelum kita berbicara tentang menyelesaikannya, kita perlu berbicara tentang apa itu "fungsi gelombang" ini.

Apa itu Fungsi Gelombang?

Dalam mekanika Klasik, kami menggunakan persamaan hamiltonian klasik untuk menyelesaikan persamaan gerak sebuah partikel. Persamaan gerak hanyalah persamaan di mana sebuah partikel berada pada saat tertentu dalam waktu. Misalnya, persamaan gerak partikel bebas adalah x(t)=vt + x0. Kita dapat menemukan posisi partikel setiap saat jika kita memiliki posisi awal dan kecepatan. Dalam mekanika kuantum, kami malah menggunakan persamaan Schrodinger untuk menemukan sesuatu yang disebut "fungsi gelombang". Fungsi gelombang itu sendiri tidak bermakna secara fisik — tidak berarti apa-apa dan tidak memberi tahu Anda apa pun (secara langsung). Yang bermakna adalah kuadrat dari fungsi gelombang yang memberi Anda kerapatan probabilitas. Kepadatan probabilitas hanyalah sebuah fungsi yang memberi tahu Anda kemungkinan Anda menemukan partikel dalam rentang tertentu saat Anda mengukurnya. Jadi kita dapat mengatakan bahwa fungsi gelombang hanyalah "akar kuadrat" dari kerapatan probabilitas. Sekarang kita akhirnya memiliki semua latar belakang pengetahuan untuk membicarakan apa itu persamaan Schrodinger .

Seperti yang dapat kita lihat dari persamaan di atas, semuanya konstan kecuali energi potensial V(x). Kami mengambil energi potensial tertentu, dan menyelesaikan persamaan untuk kasus di mana Anda memiliki energi potensial tertentu. Ini sangat indah, karena tidak peduli tekanan apa yang ada pada sistem Anda, atau panas, muatan, voltase, apa saja — Anda tidak perlu memperhitungkan semua itu. Yang perlu Anda ketahui hanyalah fungsi energi potensial dan Anda dapat menyelesaikan persamaannya

(Jika kita ingin bertele-tele di sini, kita dapat mengatakan bahwa "secara teknis", kita memasukkan semua hal itu ke dalam potensi itu sendiri. Juga, segitiga terbalik adalah kependekan dari turunan kedua)

Perhitungan

(jika Anda tidak suka kalkulus, Anda dapat melewati bagian ini)

Sekarang, mari selesaikan persamaan Schrodinger untuk potensial sederhana dengan V(x)=0 di mana-mana. Ini dikenal sebagai partikel bebas, karena gaya total di atasnya adalah nol. Ini bebas dari semua penindasan! Dalam kasus klasik, persamaan gerak adalah x(t)=vt + x0 yang membentuk garis lurus pada grafik ruang-waktu. Mari kita lihat seperti apa fungsi gelombang untuk kasus kuantum.

Karena V(x)=0, maka persamaan schrodinger menjadi

-h²/2m(d² ψ/dx²) = Eψ

Kami kemudian dapat melakukan beberapa penataan ulang dan mendapatkan

d² ψ/dx² = -2mEψ/h²

Kita sekarang dapat melihat bahwa semua suku di ruas kanan adalah konstan kecuali ψ. Ini bagus karena membuat persamaan mudah dipecahkan. Kita kemudian dapat mendefinisikan konstanta k menjadi sqrt(2mE/h), yang berarti kita sekarang memilikinya

d²ψ / dx² = -k²ψ

Kami kemudian menambahkan kedua sisi persamaan dengan istilah tangan kanan

d²ψ/dx² + k²ψ = 0

Kami kemudian berasumsi bahwa ψ(x) = exp(rx)

dan dari sini kita dapatkan

r=-k², r= +ik atau -ik

Ini berarti bahwa ψ( x)=exp(ikx) atau

ψ( x)=exp(-ikx)

Karena persamaannya linier, kita dapat mengambil superposisi (kombinasi linier) dari kedua bagian untuk mendapatkan solusi umumnya

ψ(x) = Aexp(ikx) + Bexp(-ikx)

dan secara teknis kami selesai. Anda mungkin bertanya-tanya bagaimana kami dapat menentukan konstanta A dan B. Kami biasanya melakukan ini dengan sesuatu yang disebut normalisasi, tapi itu cerita untuk lain waktu. Ternyata untuk skenario ini tidak bisa dinormalisasi. Itu bahasa mewah untuk fungsi gelombang tidak mendekati nol saat Anda menuju tak terhingga atau minus tak terhingga. Jadi untuk nilai A dan B apa yang sesuai dengan keadaan ini? Ternyata ini bukan keadaan yang memungkinkan karena Anda tidak dapat menormalkannya. Ups!

Jangan khawatir! Ternyata superposisi dari semua kemungkinan fungsi gelombang dapat menghasilkan keadaan nyata. Ini membawa banyak hal kerennya sendiri - tetapi itu juga cerita untuk lain kali.

Terima kasih sudah membaca! Situs web ini melakukan pekerjaan yang buruk dalam memformat simbol matematika, sehingga beberapa teks matematika tidak ditampilkan dengan baik. Jika Anda ingin melihat turunan video dari hal yang sama, saya telah membuat video di sini di saluran saya Fermion Physics tentang solusinya (walaupun saya berbicara cukup cepat). Beralih antara video dan artikel ini akan membantu membuat solusi lebih jelas. Sampai Lain waktu!