Por Férmion Física

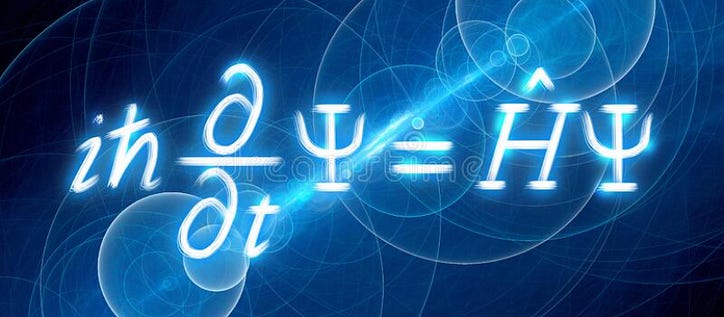
Se você estudou física quântica, ou pelo menos já ouviu falar sobre ela, pode ter ouvido falar desse tal de Schrodinger. Você sabe - aquele com toda a coisa do gato? Bem, ele também é o cara por trás de uma das equações mais úteis da mecânica quântica — a equação de Schrödinger. À primeira vista, a equação pode parecer impossível de resolver (e, de fato, em alguns casos, é!), mas depois de ler isso, você entenderá a equação e até como resolvê-la para um cenário. Preparar? Vamos.

Aqui está a equação. Parece assustador - tem até forcados! Mas vamos tentar ganhar alguma intuição nesta equação. Começaremos falando sobre energia na mecânica quântica, promovendo-a aos operadores e depois falando sobre o papel da função de onda. Depois disso, vamos juntar tudo e resolver a equação.

Mecânica Clássica

Na mecânica clássica (e mecânica quântica), a fórmula para energia é E = KE + PE onde E é a energia total, KE é a energia cinética e PE é a energia potencial. Agora KE e PE demoram um pouco para escrever, então, para economizar alguns milissegundos de escrita, os físicos usam os símbolos óbvios de T e V para representar a energia cinética e potencial, respectivamente. Então agora temos que E = T + V

Nota de rodapé: Se você estudou mecânica clássica, pode notar que estamos usando a formulação hamiltoniana! Trataremos da formulação lagrangiana outro dia.

Agora sabemos que T=p²/2m (fórmula da energia cinética). Aqui, m=massa, p=momento, e o símbolo mais difícil de todos, ½=metade. A massa é sempre constante, mas o momento não precisa ser. Se alguém aplicar uma força a um objeto, o momento começará a mudar e se desviará de seu valor original. Agora, e quanto à energia potencial?

A fórmula para a energia potencial é V= -(integral de F) onde F é a força. Torna-se evidente que a energia potencial depende da força aplicada a um objeto. Em diferentes cenários, sua energia potencial pode assumir valores diferentes, pois existem forças diferentes. Por exemplo, em um poço gravitacional, o potencial é V=mgx, mas em um oscilador harmônico, o potencial se torna V=(1/2)kx². Isso é muito importante porque nossos “cenários” para onde resolvemos nossa equação de Schrödinger são, na verdade, apenas potenciais diferentes. Isso fará sentido mais tarde.

Primeira Quantização

Agora, na mecânica quântica, pegamos nossos “observáveis” (T e E) e os fazemos ter operadorhomólogos. Um operador para nossos propósitos é apenas uma função que recebe um valor e devolve outro. Portanto, T tem uma contraparte do operador de energia cinética, geralmente denotada por um T', e a energia assume uma contraparte do operador de energia, geralmente denotada com um H. A energia potencial é "dada" em vez de resolvida, portanto, não tem nenhuma correspondente do operador. Já o operador de energia cinética é definido como um operador onde ao atuar sobre a função de onda, retorna a energia cinética da partícula multiplicada pela função de onda. A mesma coisa com a operadora de Energia. Tudo isso pode parecer um pouco inútil e abstrato, mas acredite em mim não é - estamos chegando lá. Agora lembra como T=(1/2m)p²? Isso implica que T' = (1/2m)p̂², onde p̂ é o operador do momento . E como antes, p̂ ψ = p ψonde p é o momento da partícula (novamente, um operador atua em uma função e retorna a função multiplicada por qualquer valor relacionado ao operador). Agora acontece que o operador de momento é

p̂ = -ih(d/dx). Tome isso como certo por enquanto. Isso implica que

T' = -h²/2m (d²/dx²). E como E = T + V, então H=(-h²/2m)(d²/dx²) + V. Agora podemos multiplicar ambos os lados pela função de onda para obter

H ψ = -h²/2m (d²ψ/dx²) + Vψ

E lembre-se de antes, H ψ = Eψ, então

E ψ = (-h²/2m)(d²ψ/dx²) + Vψ

Agora respire fundo. Fizemos muitas contas e esperamos que você não esteja perdido. Acontece que acabamos de “derivar” a equação de Schrödinger! Agora, antes de falarmos sobre como resolvê-lo, precisamos falar sobre o que é essa “função de onda”.

O que é uma função de onda?

Na mecânica clássica, usamos a equação hamiltoniana clássica para resolver as equações do movimento de uma partícula. As equações de movimento são apenas as equações para onde uma partícula está em um determinado momento no tempo. Por exemplo, a equação de movimento para uma partícula livre é x(t)=vt + x0. Podemos encontrar a posição da partícula para qualquer momento no tempo se tivermos a posição inicial e a velocidade. Na mecânica quântica, usamos a equação de Schrödinger para encontrar algo chamado “função de onda”. A função de onda em si não é fisicamente significativa - não significa nada e não diz nada (diretamente). O que é significativo é o quadrado da função de onda que lhe dá a densidade de probabilidade. A densidade de probabilidade é apenas uma função que informa a chance de você encontrar uma partícula em algum intervalo ao medi-la. Então podemos dizer que a função de onda é apenas a “raiz quadrada” da densidade de probabilidade. Agora finalmente temos todo o conhecimento básico para falar sobre o que é a equação de Schrödinger .

Como podemos ver na equação acima, tudo é constante, exceto a energia potencial V(x). Pegamos uma energia potencial específica e resolvemos a equação para o caso em que você tem essa energia potencial específica. Isso é tão bonito, porque não importa quais tensões existem em seu sistema, ou calor, carga, voltagem, o que você quiser - você não precisa levar em conta nada disso. Tudo que você precisa saber é apenas a função de energia potencial e você pode resolver a equação

(Se quisermos ser pedantes aqui, poderíamos dizer que “tecnicamente”, estamos incorporando todas essas coisas dentro do próprio potencial. Além disso, o triângulo invertido é a abreviação da segunda derivada)

Cálculo

(se você não gosta de cálculo, pode pular esta parte)

Agora, vamos resolver a equação de Schrödinger para um potencial simples onde V(x)=0 em todos os lugares. Isso é conhecido como partícula livre, pois as forças resultantes sobre ela são zero. Está livre de toda opressão! No caso clássico, a equação de movimento seria x(t)=vt + x0 que forma uma linha reta em um gráfico de espaço-tempo. Vamos ver como é a função de onda para o caso quântico.

Como V(x)=0, então a equação de Schrödinger se torna

-h²/2m(d² ψ/dx²) = Eψ

Podemos então fazer alguma reorganização e obter

d² ψ/dx² = -2mEψ/h²

Agora podemos ver que todos os termos do lado direito são constantes, exceto ψ. Isso é bom porque torna a equação fácil de resolver. Podemos então definir uma constante k como sqrt(2mE/h), o que significa que agora temos

d²ψ / dx² = -k²ψ

Em seguida, adicionamos ambos os lados da equação pelo termo à direita

d²ψ/dx² + k²ψ = 0

Assumimos então que ψ(x) = exp(rx)

e disso obtemos

r=-k², r= +ik ou -ik

Isso significa que ψ( x)=exp(ikx) ou

ψ( x)=exp(-ikx)

Como a equação é linear, podemos fazer uma superposição (combinação linear) de ambas as partes para obter a solução geral

ψ(x) = Aexp(ikx) + Bexp(-ikx)

e terminamos tecnicamente. Você pode estar se perguntando como podemos determinar as constantes A e B. Normalmente faríamos isso por meio de algo chamado normalização, mas essa é uma história para outra hora. Acontece que para este cenário não pode ser normalizado. Essa é uma linguagem sofisticada para a função de onda não se aproximar de zero à medida que você vai para o infinito ou menos infinito. Então, para quais valores A e B correspondem a esse estado? Bem, acontece que este não é realmente um estado possível, já que você não pode normalizá-lo. Ops!

Não se preocupe! Acontece que uma superposição de todas as funções de onda possíveis pode produzir um estado real. Isso traz muitas coisas legais - mas isso também é uma história para a próxima vez.

Obrigado por ler! Este site faz um péssimo trabalho na formatação de símbolos matemáticos, então parte do texto matemático não apareceu bem. Se você quiser ver uma derivação em vídeo da mesma coisa, fiz um vídeo aqui no meu canal Fermion Physics sobre a solução (embora eu fale bem rápido). Alternar entre o vídeo e este artigo ajudará a tornar a solução mais clara. Até a próxima!