
NBA koçu ve eski oyuncu Jason Kidd'e atfedilen meşhur bir söz var : "Bu takımı 360 derece döndüreceğiz!"
Vay canına. Matematik öğretmenleri buna gözlerini devirmiş olmalı.
Bildiğiniz gibi, bir daire tam olarak 360 dereceden oluşur. Kidd sözünü tutmuş olsaydı, ekibi her şeyi yoluna koyardı. Sorun şu ki, takım "tam bir daire çizip" başladığı yere geri dönene kadar dönmeyi bırakmayacaktı .
İyileştirme tarifi değil. Kidd'in aradığı şey, takımını 180 derece döndürmek ve onları kazanan yapmaktı!
Dereceler, Tanımlı
Derece , bu bağlamda açıları ölçmek için kullanabileceğimiz bir birimdir . Kağıt üzerinde dereceler, şuna benzeyen derece sembolü ile temsil edilir: °
Yani " 18 derece" yazmak yerine " 18 ° " yazabilirsiniz .
Trigonometri ve geometrideki en önemli kavramlardan biri dik açıdır . Bu, iki dik doğrunun kesiştiği yerde oluşan açıdır .
Aynı zamanda tam bir dönüşün dörtte birini temsil eder.
Diyelim ki bir şeyi fiziksel olarak dönüştürmek istiyorsunuz. Herhangi bir şey. Sabit bir merkez noktası seçtiniz ve bu nesneyi dairesel bir hareketle etrafında döndürmeye çalışıyorsunuz. İşi bitirir ve tam bir daire çizerseniz, bu tam bir dönüş. Ancak süreci yüzde 25 oranında durdurursanız, bu tam bir dönüşün yalnızca dörtte biri demektir. Bu da size doğru bir açı verir.
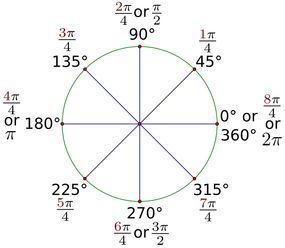
Bir dik açı 90 dereceye eşittir (yani 360'ın yüzde 25'i). Bunu ifade etmenin başka bir yolu : Bir dik açı π/2 radyana eşittir .
Zaman aşımı! radyan nedir? Ve π ( pi ) buna nasıl karıştı?
Radyanları Paketten Çıkarma
Tamam, mükemmel bir daire hayal edin. Tam merkezinde başlayan ve dairenin kavisli çevresinde (dış kenarda olduğu gibi) biten düz bir çizgi vardır.
Tanım olarak, bu doğru dairemizin yarıçapıdır .
Esasen, bir radyan bir daire dilimidir. Dairenin kavisli dış çevresine bir kez daha bakın. Şimdi, çemberinizin yarıçapına eşit uzunlukta bir çevre parçası hayal edin. İki uç noktasını dairenin tam merkezine bağlayan iki düz çizgi çizerseniz, üretecekleri açı bir radyan olur.
Her çemberde aynı sayıda radyan için yer vardır. Bu sayı 2 çarpı pi'ye ("π") eşittir. Pi'nin kendisi yaklaşık 3.14'e eşit olduğundan, bir daire içinde yaklaşık 6.28 radyan (2 x 3.14) olduğunu söyleyebilirsiniz. Veya 1 radyan yaklaşık 57.29 derecedir (180°/π).
Radyan Vs. derece
Bak, inkar etmeyeceğiz. Radyan, görselleştirilmesi derecelere göre daha zor bir kavram olabilir.
Ama ilkini küçümsemeyin. Bu açı ölçüm birimlerinin her ikisinin de avantajları vardır.
Derece çok daha popüler. Gerçek dünyada, radyan yerine derece açısından düşünen insanlarla karşılaşmanız daha olasıdır. Yani, matematikçi olmayan biriyle iletişim kurmaya çalışıyorsanız, belki derecelere bağlı kalın.
Bununla birlikte, matematikte radyanlar harikadır çünkü kendilerini çok daha basit denklemlere borçludurlar . Gelecekteki AP öğrencileri bunu akıllarında tutmak isteyeceklerdir.
Dereceleri Radyana Dönüştürme (ve Tersi)
Dereceleri radyana dönüştürmek için birkaç kolay adımı ezberlemeniz yeterlidir.
İlk olarak, dönüştürmek istediğiniz derece sayısını alın. Bu sayıyı π radyan/180 derece ile çarpın . Bazı gereksiz birimleri ortadan kaldırarak ve ardından işleri biraz basitleştirerek, cevabınızı alacaksınız.
120 derecelik bir açıyla bükülmüş bir metal çubuğunuz olduğunu varsayalım. Bunu radyan cinsinden nasıl ifade edebiliriz?
Bunu bulmak için denklemimizi şu şekilde yazacağız:
120 ° x (π radyan/180 ° )
Yukarıda gösterilen derece sembolü çiftine dikkat edin. Bunlar birbirini iptal edecek ve nihai cevabımızın radyan cinsinden olmasını sağlayacaktır. Artık elimizde:
120 x (π radyan/180)
Çarpmayı yapın ve 120π/180 radyan elde edin . Ama daha işimiz bitmedi. Şimdi kesirimizi mümkünse sadeleştirmemiz gerekiyor. Hem paydaya (180) hem de payın (120) π olmayan kısmına tam olarak bölünebilecek en yüksek tam sayıyı belirlememiz gerekiyor. Spoiler uyarısı: Bizim durumumuzda sihirli sayı 60'tır.
120π ve 180'i 60'a bölerseniz, 2π/3 radyan elde edersiniz.
İşte başlıyoruz: 120°, 2π/3 radyana eşittir.
Radyandan dereceye gitmek de benzer bir işlemdir . Sadece bu durumda, başlangıç radyan miktarını alır ve (180 ° / π ) ile çarpardık.
π/3 radyan x (180 ° / π) = 60 derece
Özetlemek:
Radyandan dereceye çevirmek için : 180 ile çarpın, π ile bölün
Dereceden radyana çevirmek için : π ile çarpın, 180'e bölün
Şimdi Bu İlginç
Aynı merkezi paylaşan iki eş merkezli daireden oluşan "halka" şekline teknik olarak " halka " denir .















































