
Há uma citação infame atribuída ao técnico da NBA e ex-jogador Jason Kidd: "Vamos virar esse time em 360 graus!"
Opa. Os professores de matemática devem ter revirado os olhos para isso.
Como você já deve saber, um círculo é feito exatamente de 360 graus. Se Kidd tivesse cumprido sua promessa, então sua equipe teria dado a volta por cima. O problema é que o esquadrão não parava de girar até que tivesse "feito o círculo completo" e acabasse de volta onde começou.
Não é uma receita para melhorar. O que Kidd estava procurando era virar sua equipe em 180 graus e torná-los vencedores!
Graus, Definidos
O grau , neste contexto, é uma unidade que podemos usar para medir ângulos . No papel, os graus são representados pelo símbolo de grau, que se parece com isso: °
Então, em vez de escrever " 18 graus", você pode simplesmente escrever " 18 ° " .
Um dos conceitos mais importantes em trigonometria e geometria é o ângulo reto . Este é o ângulo formado onde duas linhas perpendiculares se cruzam.
Também representa um quarto de uma rotação completa.
Digamos que você queira transformar algo fisicamente. Nada. Você escolheu um ponto central fixo e está tentando manobrar esse objeto em torno dele em um movimento circular. Se você terminar o trabalho e fizer um círculo completo, é uma rotação completa. Mas se você interromper o processo em 25% do caminho, isso representa apenas um quarto de uma rotação completa. O que lhe dá um ângulo reto.
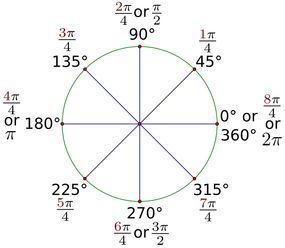
Um ângulo reto é igual a 90 graus (ou seja, 25 por cento de 360). Aqui está outra maneira de colocar : Um ângulo reto é igual a π/2 radianos .
Tempo esgotado! O que é um radiano? E como π ( pi ) se misturou nisso?
Desempacotando radianos
OK, imagine um círculo perfeito. Há uma linha reta que começa em seu centro exato e termina no perímetro curvo do círculo (como na borda externa).
Por definição, essa linha é o raio do nosso círculo.
Essencialmente, um radiano é uma fatia de um círculo. Olhe para o perímetro externo curvo do círculo mais uma vez. Agora imagine um segmento do perímetro que é igual em comprimento ao raio do seu círculo. Se você desenhasse duas linhas retas conectando suas duas extremidades ao centro exato do círculo, o ângulo que elas produziriam seria um radiano.
Cada círculo tem espaço para o mesmo número de radianos. Esse número é igual a 2 vezes pi ("π"). Como o próprio pi é igual a cerca de 3,14, você poderia dizer que há aproximadamente 6,28 radianos em um círculo (2 x 3,14). Ou que 1 radiano é cerca de 57,29 graus (180°/π).
Radianos vs. Graus
Olha, não vamos negar. Os radianos podem ser um conceito mais difícil de visualizar do que os graus.
Mas não desconte o primeiro. Ambas as unidades de medição de ângulos têm suas vantagens.
O grau é muito mais popular. No mundo real, é mais provável que você encontre pessoas que pensam em termos de graus em vez de radianos. Então, se você está tentando se comunicar com um não-matemático, talvez fique com os diplomas.
No entanto, em cálculo, radianos são ótimos porque se prestam a equações muito mais simples . Os futuros alunos do AP vão querer manter isso em mente.
Convertendo graus para radianos (e vice-versa)
Para converter graus em radianos, você só precisa memorizar alguns passos fáceis.
Primeiro, pegue o número de graus que você deseja converter. Multiplique este número por π radianos/180 graus . Eliminando algumas unidades redundantes e simplificando um pouco as coisas, você terá sua resposta.
Suponha que você tenha uma barra de metal que foi dobrada em um ângulo de 120 graus. Como podemos expressar isso em termos de radianos?
Para descobrir, vamos escrever nossa equação assim:
120 ° x (π radianos/180 ° )
Observe o par de símbolos de grau mostrados acima. Esses se cancelarão, garantindo que nossa resposta final seja em radianos. Agora nos resta:
120 x (π radianos/180)
Faça a multiplicação e você terá 120π/180 radianos . Mas ainda não terminamos. Agora temos que simplificar nossa fração, se possível. Precisamos identificar o número inteiro mais alto que pode ser dividido exatamente no denominador (180) e na parte não π do numerador (120). Alerta de spoiler: no nosso caso, o número mágico é 60.
Se você realmente dividir 120π e 180 por 60, obterá 2π/3 radianos.
Então, vamos lá: 120° é igual a 2π/3 radianos.
Passar de radianos para graus é um procedimento semelhante . Somente neste caso, pegaríamos a quantidade inicial de radianos e a multiplicaríamos por (180 ° / π ).
π/3 radianos x (180 ° / π) = 60 graus
Para resumir:
Para converter de radianos para graus : multiplique por 180, divida por π
Para converter de graus para radianos : multiplique por π, divida por 180
Agora isso é interessante
A forma de "anel", composta por dois círculos concêntricos que compartilham o mesmo centro, é tecnicamente chamada de " anular ".















































