
C'è una famigerata citazione attribuita all'allenatore della NBA ed ex giocatore Jason Kidd: "Faremo girare questa squadra di 360 gradi!"
Ops. Gli insegnanti di matematica devono aver alzato gli occhi al cielo.
Come forse già saprai, un cerchio è composto esattamente da 360 gradi. Se Kidd avesse mantenuto la sua promessa, la sua squadra si sarebbe girata bene. Il problema è che la squadra non avrebbe smesso di girare fino a quando non avesse "fatto il giro completo" e fosse tornata al punto di partenza.
Non una ricetta per il miglioramento. Quello che Kidd stava cercando era trasformare la sua squadra di 180 gradi e renderla vincente!
Gradi, Definiti
Il grado , in questo contesto, è un'unità che possiamo usare per misurare gli angoli . Sulla carta, i gradi sono rappresentati dal simbolo del grado, che si presenta così: °
Quindi, invece di scrivere " 18 gradi", potresti semplicemente scrivere " 18 ° " .
Uno dei concetti più importanti in trigonometria e geometria è l' angolo retto . Questo è l'angolo formato all'intersezione di due rette perpendicolari .
Rappresenta anche un quarto di una rotazione completa.
Diciamo che vuoi trasformare fisicamente qualcosa. Nulla. Hai scelto un punto centrale fisso e stai cercando di manovrare quell'oggetto attorno ad esso con un movimento circolare. Se finisci il lavoro e fai un cerchio completo, è una rotazione completa. Ma se interrompi il processo al 25 percento, è solo un quarto di una rotazione completa. Che ti dà un angolo retto.
Un angolo retto è uguale a 90 gradi (cioè il 25 percento di 360). Ecco un altro modo per dirla : un angolo retto è uguale a π/2 radianti .
Tempo scaduto! Cos'è un radiante? E come ha fatto π ( pi ) a confondersi in questo?
Disimballaggio dei radianti
OK, immagina un cerchio perfetto. C'è una linea retta che inizia al suo centro esatto e termina al perimetro curvo del cerchio (come in, il bordo esterno).
Per definizione, quella linea è il raggio del nostro cerchio.
In sostanza, un radiante è una fetta di un cerchio. Osserva ancora una volta il perimetro esterno curvo del cerchio. Ora immagina un segmento del perimetro che sia uguale in lunghezza al raggio del tuo cerchio. Se disegnassi due linee rette che collegano i suoi due estremi al centro esatto del cerchio, l'angolo che produrrebbero sarebbe un radiante.
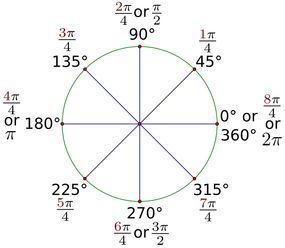
Ogni cerchio ha spazio per lo stesso numero di radianti. Quel numero è uguale a 2 volte pi ("π"). Poiché pi stesso è uguale a circa 3,14, puoi dire che ci sono circa 6,28 radianti in un cerchio (2 x 3,14). O che 1 radiante è di circa 57,29 gradi (180°/π).
Radianti vs. Gradi
Guarda, non lo negheremo. I radianti possono essere un concetto più difficile da visualizzare rispetto ai gradi.
Ma non scartare il primo. Entrambe queste unità di misura dell'angolo hanno i loro vantaggi.
Il grado è molto più popolare. Nel mondo reale, è più probabile incontrare persone che pensano in termini di gradi anziché in radianti. Quindi, se stai cercando di comunicare con un non matematico, forse attieniti ai gradi.
Tuttavia, nel calcolo, i radianti sono ottimi perché si prestano a equazioni molto più semplici . I futuri studenti AP vorranno tenerlo a mente.
Conversione dei gradi in radianti (e viceversa)
Per convertire i gradi in radianti, devi solo memorizzare alcuni semplici passaggi.
Innanzitutto, prendi il numero di gradi che desideri convertire. Moltiplica questo numero per π radianti/180 gradi . Eliminando alcune unità ridondanti e quindi semplificando un po' le cose, avrai la tua risposta.
Supponiamo di avere una barra di metallo piegata con un angolo di 120 gradi. Come possiamo esprimere questo in termini di radianti?
Per scoprirlo, scriveremo la nostra equazione in questo modo:
120 ° x (π radianti/180 ° )
Notare la coppia di simboli dei gradi mostrati sopra. Quelli si annulleranno a vicenda, assicurandoci che la nostra risposta finale sarà in radianti. Ora ci rimane:
120 x (π radianti/180)
Fai la moltiplicazione e ottieni 120π/180 radianti . Ma non abbiamo ancora finito. Ora dobbiamo semplificare la nostra frazione, se possibile. Dobbiamo identificare il numero intero più alto che può essere diviso esattamente sia nel denominatore (180) che nella parte non π del numeratore (120). Avviso spoiler: nel nostro caso, il numero magico è 60.
Se dividi effettivamente 120π e 180 per 60, ottieni 2π/3 radianti.
Quindi, eccoci qua: 120° è uguale a 2π/3 radianti.
Passare dai radianti ai gradi è una procedura simile . Solo in questo caso, prendiamo la quantità iniziale di radianti e la moltiplichiamo per (180 ° / π ).
π/3 radianti x (180 ° / π) = 60 gradi
Riassumere:
Per convertire da radianti a gradi : moltiplicare per 180, dividere per π
Per convertire da gradi a radianti : moltiplicare per π, dividere per 180
Ora è interessante
La forma ad "anello", composta da due cerchi concentrici che condividono lo stesso centro, è tecnicamente chiamata " annulus ".















































