วิธีการแปลงองศาเป็นเรเดียนอย่างง่ายดาย (และเรเดียนเป็นองศา)

มีคำพูดที่น่าอับอายมาจากโค้ช NBA และอดีตผู้เล่น Jason Kidd: "เราจะเปลี่ยนทีมนี้ให้รอบ 360 องศา!"

อ๊ะ ครูคณิตศาสตร์ต้องกลอกตาไปที่ตัวนั้น

อย่างที่คุณอาจทราบแล้ววงกลมประกอบด้วย 360 องศาพอดี ถ้าคิดด์ทำตามสัญญา ทีมงานของเขาก็คงหันหลังกลับ ปัญหาคือ ทีมจะไม่หยุดหมุนจนกว่ามันจะ "เต็มวง" และจบลงที่จุดเริ่มต้น

ไม่ใช่สูตรสำหรับการปรับปรุง สิ่งที่ Kidd กำลังมองหาคือทำให้ทีมของเขาหมุนไปรอบ ๆ 180 องศาและทำให้พวกเขาเป็นผู้ชนะ!

องศาที่กำหนด

องศาในบริบทนี้เป็นหน่วยที่เราสามารถใช้วัดมุมได้ บนกระดาษ องศาจะแสดงด้วยสัญลักษณ์องศา ซึ่งมีลักษณะดังนี้: °

ดังนั้น แทนที่จะเขียนว่า " 18 องศา"คุณก็เขียนว่า " 18 °ได้เลย "

แนวคิดที่สำคัญที่สุดประการหนึ่งในตรีโกณมิติและเรขาคณิตคือมุมฉาก นี่คือมุมที่เกิดขึ้นโดยที่เส้นตั้งฉากสองเส้นตัดกัน

มันยังแสดงถึงหนึ่งในสี่ของการหมุนทั้งหมด

สมมติว่าคุณต้องการพลิกบางอย่างทางกายภาพ อะไรก็ตาม. คุณได้เลือกจุดศูนย์กลางที่ตายตัวแล้วและกำลังพยายามเคลื่อนวัตถุรอบๆ ตัวเป็นวงกลม หากคุณทำงานเสร็จและหมุนเป็นวงกลม แสดงว่าเป็นการหมุนเวียนที่สมบูรณ์ แต่ถ้าคุณหยุดกระบวนการ 25 เปอร์เซ็นต์ของกระบวนการ นั่นคือเพียงหนึ่งในสี่ของการหมุนทั้งหมด ซึ่งให้มุมฉากกับคุณ

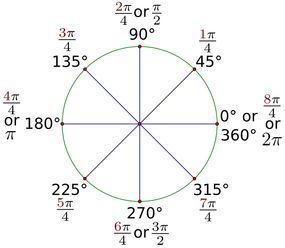
มุมฉากเท่ากับ 90 องศา (เช่น 25 เปอร์เซ็นต์ของ 360) นี่เป็นอีกวิธีหนึ่งในการวาง : มุมฉากเท่ากับ π/ 2 เรเดียน

หมดเวลา! เรเดียนคืออะไร? แล้ว π ( pi ) มารวมกันได้อย่างไร?

แกะเรเดียน

ตกลง ลองนึกภาพวงกลมที่สมบูรณ์แบบ มีเส้นตรงที่เริ่มต้นจากจุดศูนย์กลางที่แน่นอนและสิ้นสุดที่ขอบโค้งของวงกลม (เช่นใน ขอบด้านนอก)

ตามนิยาม เส้นนั้นคือรัศมีของวงกลมของเรา

โดยพื้นฐานแล้ว เรเดียนคือเสี้ยวของวงกลม ดูเส้นรอบวงด้านนอกโค้งของวงกลมอีกครั้ง ทีนี้ลองนึกภาพส่วนของเส้นรอบรูปที่มีความยาวเท่ากับรัศมีวงกลมของคุณ หากคุณวาดเส้นตรงสองเส้นที่เชื่อมจุดปลายทั้งสองเข้ากับจุดศูนย์กลางที่แน่นอนของวงกลม มุมที่พวกมันจะสร้างได้จะเป็นเรเดียน

ทุกวงกลมมีที่ว่างสำหรับจำนวนเรเดียนเท่ากัน จำนวนนั้นเท่ากับ 2 คูณ pi ("π") เนื่องจาก pi เองมีค่าเท่ากับ 3.14 คุณจึงอาจกล่าวได้ว่าวงกลมมีประมาณ 6.28 เรเดียน (2 x 3.14) หรือ 1 เรเดียนนั้นมีค่าประมาณ 57.29 องศา (180°/π)

เรเดียน VS. องศา

ฟังนะ เราจะไม่ปฏิเสธ เรเดียนอาจเป็นแนวคิดที่มองเห็นได้ยากกว่าองศา

แต่อย่าลดอดีต หน่วยวัดมุมทั้งสองนี้มีข้อดีของตัวเอง

องศาเป็นที่นิยมมากขึ้น ในโลกแห่งความเป็นจริง คุณมักจะพบกับคนที่คิดในแง่ดีกรีมากกว่าเรเดียน ดังนั้น หากคุณกำลังพยายามสื่อสารกับผู้ที่ไม่ใช่นักคณิตศาสตร์ ให้ยึดเอาดีกรี

อย่างไรก็ตาม ในแคลคูลัส เรเดียนนั้นยอดเยี่ยมเพราะพวกมันใช้สมการที่ง่ายกว่ามาก นักเรียน AP ในอนาคตจะต้องจำไว้เสมอ

การแปลงองศาเป็นเรเดียน (และในทางกลับกัน)

ในการแปลงองศาเป็นเรเดียน คุณเพียงแค่ต้องจำขั้นตอนง่ายๆ ไม่กี่ขั้นตอน

ขั้นแรก หาจำนวนองศาที่คุณต้องการแปลง คูณตัวเลขนี้ด้วย π เรเดียน/180องศา การกำจัดหน่วยที่ซ้ำซ้อนออกไปแล้วลดความซับซ้อนลงเล็กน้อย คุณจะได้คำตอบ

สมมติว่าคุณมีแท่งเหล็กดัดเป็นมุม 120 องศา เราจะแสดงออกในรูปของเรเดียนได้อย่างไร?

เพื่อหา เราจะเขียนสมการของเราดังนี้:

120 ° x (π เรเดียน/180 ° )

สังเกตคู่ของสัญลักษณ์องศาที่แสดงด้านบน สิ่งเหล่านี้จะหักล้างซึ่งกันและกัน เพื่อให้แน่ใจว่าคำตอบสุดท้ายของเราจะเป็นหน่วยเรเดียน ตอนนี้เราเหลือ:

120 x (π เรเดียน/180)

ทำการคูณแล้วคุณจะได้120π /180 เรเดียน แต่เรายังไม่เสร็จ ตอนนี้ เราต้องลดรูปเศษส่วนถ้าเป็นไปได้ เราจำเป็นต้องระบุจำนวนเต็มสูงสุดที่สามารถแบ่งออกเป็นทั้งตัวส่วน (180) และส่วนที่ไม่ใช่ π ของตัวเศษ (120) การแจ้งเตือนผู้สปอยเลอร์: ในกรณีของเรา ตัวเลขมหัศจรรย์คือ 60

หากคุณหาร 120π และ 180 ด้วย 60 คุณจะได้ 2π/3 เรเดียน

ไปเลย: 120° เท่ากับ 2π/3 เรเดียน

การเปลี่ยนจากเรเดียนเป็นองศาเป็นขั้นตอนที่คล้ายคลึงกัน เฉพาะในกรณีนี้ เราจะหาจำนวนเรเดียนเริ่มต้นแล้วคูณด้วย (180 ° / π )

π/3เรเดียน x (180 ° / π) = 60 องศา

เพื่อสรุป:

การแปลงจากเรเดียนเป็นองศา : คูณ 180, หารด้วย π

การแปลงจากองศาเป็นเรเดียน : คูณด้วย π, หารด้วย 180

ตอนนี้น่าสนใจ

รูปร่าง "วงแหวน" ที่ประกอบด้วยวงกลมสองวงที่มีจุดศูนย์กลางเดียวกัน ในทางเทคนิคเรียกว่า " วงแหวน "