สถิติ - การกระจายเบต้า
การแจกแจงแบบเบต้าแสดงถึงการแจกแจงความน่าจะเป็นแบบต่อเนื่องที่พารามิเตอร์รูปทรงบวกสองตัวคือ $ \ alpha $ และ $ \ beta $ ซึ่งปรากฏเป็นเลขชี้กำลังของตัวแปรสุ่ม x และควบคุมรูปร่างของการแจกแจง
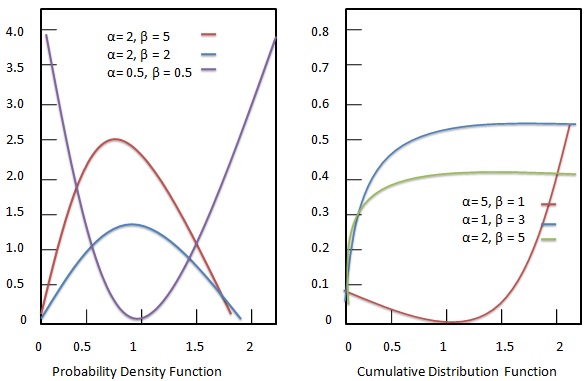
ฟังก์ชั่นความหนาแน่นของความน่าจะเป็น
ฟังก์ชันความหนาแน่นของความน่าจะเป็นของการแจกแจงเบต้าได้รับเป็น:
สูตร
$ {f (x) = \ frac {(xa) ^ {\ alpha-1} (bx) ^ {\ beta-1}} {B (\ alpha, \ beta) (ba) ^ {\ alpha + \ beta- 1}} \ hspace {.3in} a \ le x \ le b; \ alpha, \ beta> 0 \\ [7pt] \ โดยที่ \ B (\ alpha, \ beta) = \ int_ {0} ^ {1} {t ^ {\ alpha-1} (1-t) ^ { \ beta-1} dt}} $
ที่ไหน -
$ {\ alpha, \ beta} $ = พารามิเตอร์รูปร่าง
$ {a, b} $ = ขอบเขตบนและล่าง
$ {B (\ alpha, \ beta)} $ = ฟังก์ชันเบต้า
การกระจายเบต้ามาตรฐาน
ในกรณีที่มีขอบเขตบนและล่างเป็น 1 และ 0 การแจกแจงแบบเบต้าเรียกว่าการแจกแจงเบต้ามาตรฐาน ขับเคลื่อนด้วยสูตรต่อไปนี้:
สูตร
$ {f (x) = \ frac {x ^ {\ alpha-1} (1-x) ^ {\ beta-1}} {B (\ alpha, \ beta)} \ hspace {.3in} \ le x \ เลอ 1; \ alpha, \ beta> 0} $
ฟังก์ชันการแจกแจงสะสม
ฟังก์ชันการแจกแจงสะสมของการแจกแจงแบบเบต้าได้รับเป็น:
สูตร
$ {F (x) = I_ {x} (\ alpha, \ beta) = \ frac {\ int_ {0} ^ {x} {t ^ {\ alpha-1} (1-t) ^ {\ beta- 1} dt}} {B (\ alpha, \ beta)} \ hspace {.2in} 0 \ le x \ le 1; p, \ beta> 0} $
ที่ไหน -
$ {\ alpha, \ beta} $ = พารามิเตอร์รูปร่าง
$ {a, b} $ = ขอบเขตบนและล่าง
$ {B (\ alpha, \ beta)} $ = ฟังก์ชันเบต้า
เรียกอีกอย่างว่าอัตราส่วนฟังก์ชันเบต้าที่ไม่สมบูรณ์