สถิติ - การถดถอยโลจิสติก

การถดถอยโลจิสติกเป็นวิธีการทางสถิติในการวิเคราะห์ชุดข้อมูลซึ่งมีตัวแปรอิสระอย่างน้อยหนึ่งตัวที่กำหนดผลลัพธ์ ผลลัพธ์ถูกวัดด้วยตัวแปรสองขั้ว (ซึ่งมีเพียงสองผลลัพธ์ที่เป็นไปได้)

สูตร

$ {\ pi (x) = \ frac {e ^ {\ alpha + \ beta x}} {1 + e ^ {\ alpha + \ beta x}}} $

ที่ไหน -

การตอบสนอง - การมีอยู่ / ไม่มีลักษณะเฉพาะ
Predictor - ตัวแปรตัวเลขที่สังเกตได้สำหรับแต่ละกรณี
$ {\ beta = 0 \ Rightarrow} $ P (Presence) จะเท่ากันในแต่ละระดับของ x
$ {\ beta \ gt 0 \ Rightarrow} $ P (Presence) จะเพิ่มขึ้นเมื่อ x เพิ่มขึ้น
$ {\ beta = 0 \ Rightarrow} $ P (Presence) จะลดลงเมื่อ x เพิ่มขึ้น

ตัวอย่าง

Problem Statement:

แก้ไขการถดถอยโลจิสติกของปัญหาต่อไปนี้ Rizatriptan สำหรับไมเกรน

การตอบสนอง - บรรเทาอาการปวดได้อย่างสมบูรณ์ภายใน 2 ชั่วโมง (ใช่ / ไม่ใช่)

ตัวทำนาย - ปริมาณ (มก.): ยาหลอก (0), 2.5,5,10

ปริมาณ	# ผู้ป่วย	# โล่งใจ	โล่งใจ
0	67	2	3.0
2.5	75	7	9.3
5	130	29	22.3
10	145	40	27.6

Solution:

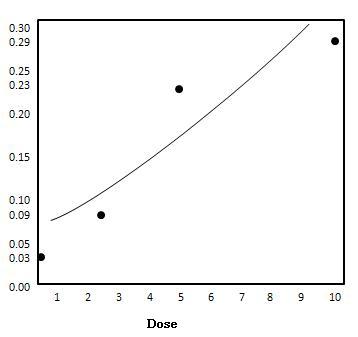
มี $ {\ alpha = -2.490} และ $ {\ beta = .165} เราได้ติดตามข้อมูล:

$ {\ pi (0) = \ frac {e ^ {\ alpha + \ beta \ times 0}} {1 + e ^ {\ alpha + \ beta \ times 0}} \\ [7pt] \, = \ frac {e ^ {- 2.490 + 0}} {1 + e ^ {- 2.490}} \\ [7pt] \\ [7pt] \, = 0.03 \\ [7pt] \ pi (2.5) = \ frac {e ^ {\ alpha + \ beta \ times 2.5}} {1 + e ^ {\ alpha + \ beta \ times 2.5}} \\ [7pt] \, = \ frac {e ^ {- 2.490 + .165 \ times 2.5} } {1 + e ^ {- 2.490 + .165 \ times 2.5}} \\ [7pt] \, = 0.09 \\ [7pt] \\ [7pt] \ pi (5) = \ frac {e ^ {\ alpha + \ beta \ times 5}} {1 + e ^ {\ alpha + \ beta \ times 5}} \\ [7pt] \, = \ frac {e ^ {- 2.490 + .165 \ times 5}} {1 + e ^ {- 2.490 + .165 \ times 5}} \\ [7pt] \, = 0.23 \\ [7pt] \\ [7pt] \ pi (10) = \ frac {e ^ {\ alpha + \ beta \ times 10}} {1 + e ^ {\ alpha + \ beta \ times 10}} \\ [7pt] \, = \ frac {e ^ {- 2.490 + .165 \ times 10}} {1 + e ^ {-2.490 + .165 \ times 10}} \\ [7pt] \, = 0.29} $

ปริมาณ ($ {x} $)	$ {\ pi (x)} $
0	0.03
2.5	0.09
5	0.23
10	0.29