สถิติ - การวิเคราะห์ที่เหลือ

การวิเคราะห์เศษเหลือใช้เพื่อประเมินความเหมาะสมของแบบจำลองการถดถอยเชิงเส้นโดยการกำหนดเศษเหลือและตรวจสอบกราฟพล็อตที่เหลือ

ที่เหลือ

ส่วนที่เหลือ ($ e $) หมายถึงความแตกต่างระหว่างค่าที่สังเกตได้ ($ y $) เทียบกับมูลค่าที่คาดการณ์ไว้ ($ \ hat y $) ทุกจุดข้อมูลมีหนึ่งที่เหลือ

พล็อตที่เหลือ

พล็อตที่เหลือคือกราฟที่ส่วนที่เหลืออยู่บนแกนตั้งและตัวแปรอิสระอยู่บนแกนนอน หากจุดกระจายแบบสุ่มรอบแกนแนวนอนแบบจำลองการถดถอยเชิงเส้นจะเหมาะสมกับข้อมูล มิฉะนั้นให้เลือกแบบจำลองที่ไม่ใช่เชิงเส้น

ประเภทของพล็อตที่เหลือ

ตัวอย่างต่อไปนี้แสดงรูปแบบบางส่วนในแปลงที่เหลือ

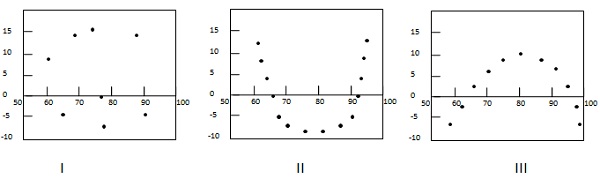
ในกรณีแรกจุดต่างๆจะกระจายแบบสุ่ม ดังนั้นจึงต้องการแบบจำลองการถดถอยเชิงเส้น ในกรณีที่สองและสามจุดจะไม่กระจายแบบสุ่มและแนะนำว่าควรใช้วิธีการถดถอยแบบไม่เป็นเชิงเส้น

ตัวอย่าง

Problem Statement:

ตรวจสอบว่าแบบจำลองการถดถอยเชิงเส้นตรงไหนเหมาะสมกับข้อมูลต่อไปนี้

$ x $	60	70	80	85	95
$ y $ (มูลค่าจริง)	70	65	70	95	85
$ \ hat y $ (ค่าที่คาดการณ์)	65.411	71.849	78.288	81.507	87.945

Solution:

Step 1: คำนวณส่วนที่เหลือสำหรับจุดข้อมูลแต่ละจุด

$ x $	60	70	80	85	95
$ y $ (มูลค่าจริง)	70	65	70	95	85
$ \ hat y $ (ค่าที่คาดการณ์)	65.411	71.849	78.288	81.507	87.945
$ e $ (ส่วนที่เหลือ)	4.589	-6.849	-8.288	13.493	-2.945

Step 2: - วาดกราฟพล็อตที่เหลือ

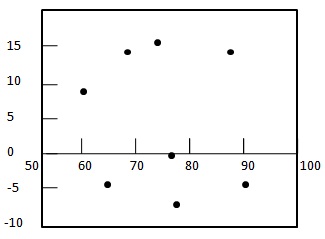
Step 3: - ตรวจสอบการสุ่มของสิ่งที่เหลือ

พล็อตที่เหลือมีรูปแบบสุ่ม - ส่วนที่เหลือแรกเป็นบวกต่อจากสองเป็นลบส่วนที่สี่เป็นบวกและส่วนที่เหลือสุดท้ายเป็นลบ เนื่องจากรูปแบบค่อนข้างสุ่มซึ่งบ่งชี้ว่าแบบจำลองการถดถอยเชิงเส้นเหมาะสมกับข้อมูลข้างต้น