สถิติ - การกระจายแกมมา

การแจกแจงแกมมาแสดงถึงการแจกแจงความน่าจะเป็นแบบต่อเนื่องของตระกูลสองพารามิเตอร์ การแจกแจงแกมมาถูกคิดค้นขึ้นโดยทั่วไปการผสมพารามิเตอร์สามชนิด

พารามิเตอร์รูปร่าง $ k $ และพารามิเตอร์มาตราส่วน $ \ theta $
พารามิเตอร์รูปร่าง $ \ alpha = k $ และพารามิเตอร์มาตราส่วนผกผัน $ \ beta = \ frac {1} {\ theta} $ เรียกว่าพารามิเตอร์อัตรา
พารามิเตอร์รูปร่าง $ k $ และพารามิเตอร์เฉลี่ย $ \ mu = \ frac {k} {\ beta} $

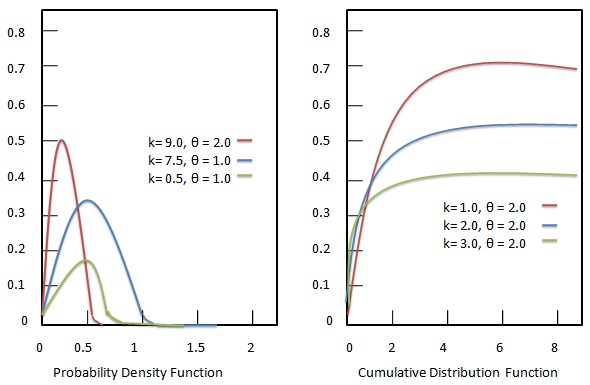
พารามิเตอร์แต่ละตัวเป็นจำนวนจริงบวก การแจกแจงแกมมาคือการแจกแจงความน่าจะเป็นเอนโทรปีสูงสุดที่ขับเคลื่อนโดยเกณฑ์ต่อไปนี้

สูตร

$ {E [X] = k \ theta = \ frac {\ alpha} {\ beta} \ gt 0 \ และ \ ได้รับการแก้ไข \\ [7pt] E [ln (X)] = \ psi (k) + ln (\ theta) = \ psi (\ alpha) - ln (\ beta) \ และ \ ได้รับการแก้ไข } $

ที่ไหน -

$ {X} $ = ตัวแปรสุ่ม
$ {\ psi} $ = ฟังก์ชัน digamma

การกำหนดลักษณะโดยใช้รูปร่าง $ \ alpha $ และให้คะแนน $ \ beta $

ฟังก์ชั่นความหนาแน่นของความน่าจะเป็น

ฟังก์ชันความหนาแน่นของความน่าจะเป็นของการแจกแจงแกมมาได้รับเป็น:

สูตร

$ {f (x; \ alpha, \ beta) = \ frac {\ beta ^ \ alpha x ^ {\ alpha - 1} e ^ {- x \ beta}} {\ Gamma (\ alpha)} \ โดยที่ \ x \ ge 0 \ and \ alpha, \ beta \ gt 0} $

ที่ไหน -