สถิติ - Boxplots

พล็อตกล่องเป็นวิธีที่เป็นมาตรฐานในการแสดงการกระจายของข้อมูลตามสรุปตัวเลขห้าตัวต่อไปนี้

1. Minimum

2. ควอร์ไทล์แรก

3. Median

4. ควอร์ไทล์ที่สาม

5. Maximum

สำหรับชุดข้อมูลที่กระจายอย่างสม่ำเสมอในแผนภาพพล็อตกล่องสี่เหลี่ยมผืนผ้ากลางจะครอบคลุมควอไทล์แรกไปยังควอไทล์ที่สาม (หรือช่วงระหว่างควอไทล์ IQR) เส้นในสี่เหลี่ยมผืนผ้าจะแสดงค่ามัธยฐานและ "หนวด" ด้านบนและด้านล่างของช่องแสดงตำแหน่งของค่าต่ำสุดและสูงสุด พล็อตกล่องดังกล่าวจะแสดงรูปแบบทั้งหมดตั้งแต่ค่าต่ำสุดไปจนถึงสูงสุดช่วงที่น่าจะเป็นรูปแบบ IQR และค่ามัธยฐาน

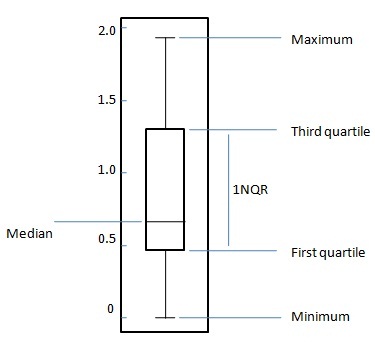
คำชี้แจงปัญหา:

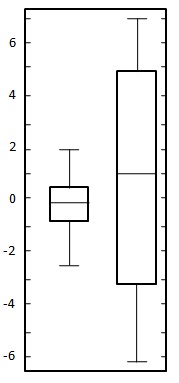
สร้างพล็อตกล่องสำหรับชุดข้อมูลสองชุดต่อไปนี้

0.22
-0.87
-2.39
-1.79
0.37
-1.54
1.28
-0.31
-0.74
1.72
0.38
-0.17
-0.62
-1.10
0.30 น
0.15
2.30
0.19
-0.50
-0.09.2018

-5.13
-2.19
-2.43
-3.83
0.50
-3.25
4.32
1.63
5.18
-0.43
7.11
4.87
-3.10
-5.81
3.76
6.31
2.58
0.07
5.76
3.50

วิธีการแก้:

ที่นี่ทั้งสองชุดข้อมูลมีความสมดุลอย่างสม่ำเสมอรอบศูนย์ดังนั้นค่าเฉลี่ยจึงอยู่ที่ประมาณศูนย์ ในรูปแบบชุดข้อมูลแรกจะมีช่วงประมาณ -2.5 ถึง 2.5 ในขณะที่ในชุดข้อมูลที่สองมีช่วงประมาณ -6 ถึง 6 วาดแผนภูมิดังที่แสดงด้านล่าง