สถิติ - Kurtosis

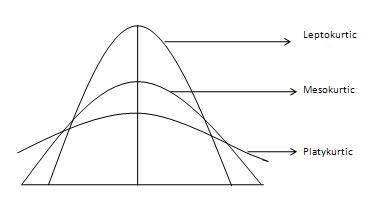
ระดับความเอียงของการกระจายวัดโดย kurtosis มันบอกให้เราทราบถึงขอบเขตที่การแจกแจงนั้นมีแนวโน้มที่จะผิดปกติ (หนักกว่าหรือเบา) มากกว่าการแจกแจงแบบปกติ เส้นโค้งสามประเภทที่ได้รับความอนุเคราะห์จาก Investopedia แสดงดังต่อไปนี้ -

เป็นการยากที่จะแยกแยะความแตกต่างของ kurtosis จากพล็อตความหนาแน่น (แผงด้านซ้าย) เนื่องจากหางอยู่ใกล้กับศูนย์สำหรับการแจกแจงทั้งหมด แต่ความแตกต่างของหางนั้นสามารถมองเห็นได้ง่ายในแปลงควอนไทล์ - ควอนไทล์ปกติ (แผงด้านขวา)

เส้นโค้งปกติเรียกว่าเส้นโค้งเมโสเคอร์ติก ถ้าเส้นโค้งของการแจกแจงมีแนวโน้มที่จะผิดปกติมากกว่า (หรือหางที่หนักกว่า) มากกว่าเส้นโค้งปกติหรือเส้นโค้งแบบ mesokurtic ก็จะเรียกว่าเส้นโค้งเลปโตเคิร์ต ถ้าเส้นโค้งมีแนวโน้มที่ผิดปกติน้อยกว่า (หรือหางที่อ่อนกว่า) กว่าเส้นโค้งปกติจะเรียกว่าเป็นเส้นโค้งแบบ platykurtic Kurtosis วัดโดยช่วงเวลาและกำหนดโดยสูตรต่อไปนี้ -

สูตร

$ {\ beta_2 = \ frac {\ mu_4} {\ mu_2}} $

ที่ไหน -

$ {\ mu_4 = \ frac {\ sum (x- \ bar x) ^ 4} {N}} $

ยิ่งค่าของ \ beta_2 มีค่าสูงสุดหรือ leptokurtic เส้นโค้งมากขึ้น เส้นโค้งปกติมีค่าเท่ากับ 3 leptokurtic มี \ beta_2 มากกว่า 3 และ platykurtic มี \ beta_2 น้อยกว่า 3

ตัวอย่าง

Problem Statement:

มีการให้ข้อมูลค่าแรงรายวันของคนงาน 45 คนของโรงงาน คำนวณ \ beta_1 และ \ beta_2 โดยใช้ช่วงเวลาเกี่ยวกับค่าเฉลี่ย แสดงความคิดเห็นเกี่ยวกับผลลัพธ์

ค่าจ้าง (Rs.)	จำนวนคนงาน
100-200	1
120-200	2
140-200	6
160-200	20
180-200	11
200-200	3
220-200	2

Solution:

ค่าจ้าง (Rs.)	จำนวนคนงาน (f)	ช่วงกลาง ม	ม - $ {\ frac {170} {20}} $ d	$ {fd} $	$ {fd ^ 2} $	$ {fd ^ 3} $	$ {fd ^ 4} $
100-200	1	110	-3	-3	9	-27	81
120-200	2	130	-2	-4	8	-16	32
140-200	6	150	-1	-6	6	-6	6
160-200	20	170	0	0	0	0	0
180-200	11	190	1	11	11	11	11
200-200	3	210	2	6	12	24	48
220-200	2	230	3	6	18	54	162
	$ {N = 45} $			$ {\ sum fd = 10} $	$ {\ sum fd ^ 2 = 64} $	$ {\ sum fd ^ 3 = 40} $	$ {\ sum fd ^ 4 = 330} $

เนื่องจากค่าเบี่ยงเบนถูกนำมาจากค่าเฉลี่ยสมมติดังนั้นเราจึงคำนวณช่วงเวลาเกี่ยวกับจุดกำเนิดโดยพลการก่อนจากนั้นจึงคำนวณช่วงเวลาเกี่ยวกับค่าเฉลี่ย ช่วงเวลาเกี่ยวกับต้นกำเนิดโดยพลการ '170'

$ {\ mu_1 ^ 1 = \ frac {\ sum fd} {N} \ times i = \ frac {10} {45} \ times 20 = 4.44 \\ [7pt] \ mu_2 ^ 1 = \ frac {\ sum fd ^ 2} {N} \ times i ^ 2 = \ frac {64} {45} \ times 20 ^ 2 = 568.88 \\ [7pt] \ mu_3 ^ 1 = \ frac {\ sum fd ^ 2} {N} \ คูณ i ^ 3 = \ frac {40} {45} \ times 20 ^ 3 = 7111.11 \\ [7pt] \ mu_4 ^ 1 = \ frac {\ sum fd ^ 4} {N} \ times i ^ 4 = \ frac {330} {45} \ คูณ 20 ^ 4 = 1173333.33} $

ช่วงเวลาเกี่ยวกับค่าเฉลี่ย

$ {\ mu_2 = \ mu'_2 - (\ mu'_1) ^ 2 = 568.88- (4.44) ^ 2 = 549.16 \\ [7pt] \ mu_3 = \ mu'_3 - 3 (\ mu'_1) (\ mu'_2) + 2 (\ mu'_1) ^ 3 \\ [7pt] \, = 7111.11 - (4.44) (568.88) + 2 (4.44) ^ 3 \\ [7pt] \, = 7111.11 - 7577.48 + 175.05 = - 291.32 \\ [7pt] \\ [7pt] \ mu_4 = \ mu'_4 - 4 (\ mu'_1) (\ mu'_3) + 6 (\ mu_1) ^ 2 (\ mu'_2) -3 (\ mu'_1) ^ 4 \\ [7pt] \, = 1173333.33 - 4 (4.44) (7111.11) +6 (4.44) ^ 2 (568.88) - 3 (4.44) ^ 4 \\ [7pt] \, = 1173333.33 - 126293.31 + 67288.03-1165.87 \\ [7pt] \, = 1113162.18} $

จากค่าของการเคลื่อนที่เกี่ยวกับค่าเฉลี่ยตอนนี้เราสามารถคำนวณ $ {\ beta_1} $ และ $ {\ beta_2} $:

$ {\ beta_1 = \ mu ^ 2_3 = \ frac {(- 291.32) ^ 2} {(549.16) ^ 3} = 0.00051 \\ [7pt] \ beta_2 = \ frac {\ mu_4} {(\ mu_2) ^ 2 } = \ frac {1113162.18} {(546.16) ^ 2} = 3.69} $

จากการคำนวณข้างต้นสรุปได้ว่า $ {\ beta_1} $ ซึ่งวัดความเบ้เกือบเป็นศูนย์จึงแสดงว่าการแจกแจงเกือบจะสมมาตร $ {\ beta_2} $ ซึ่งวัดความเคอร์โทซิสมีค่ามากกว่า 3 จึงหมายความว่าการแจกแจงเป็นโรคเลปโตคูร์ติค