สถิติ - การแจกแจงแบบไคสแควร์

การแจกแจงไคสแควร์ (ไคสแควร์หรือ $ {X ^ 2} $ - การแจกแจง) พร้อมองศาอิสระ k คือการแจกแจงผลรวมของกำลังสองของตัวแปรสุ่มปกติมาตรฐานอิสระ k เป็นการแจกแจงความน่าจะเป็นหนึ่งในสถิติที่ใช้กันอย่างแพร่หลาย เป็นกรณีพิเศษของการกระจายแกมมา

การแจกแจงแบบไคสแควร์ถูกใช้อย่างกว้างขวางโดยนักสถิติเพื่อคำนวณสิ่งต่อไปนี้:

การประมาณช่วงความเชื่อมั่นสำหรับค่าเบี่ยงเบนมาตรฐานประชากรของการแจกแจงปกติโดยใช้ค่าเบี่ยงเบนมาตรฐานตัวอย่าง
เพื่อตรวจสอบความเป็นอิสระของเกณฑ์การจำแนกสองตัวแปรเชิงคุณภาพหลายตัว
เพื่อตรวจสอบความสัมพันธ์ระหว่างตัวแปรจัดหมวดหมู่
เพื่อศึกษาความแปรปรวนของตัวอย่างที่การแจกแจงพื้นฐานเป็นปกติ
เพื่อทดสอบความเบี่ยงเบนของความแตกต่างระหว่างความถี่ที่คาดหวังและความถี่ที่สังเกตได้
เพื่อทำการทดสอบไคสแควร์ (ความดีของการทดสอบความพอดี)

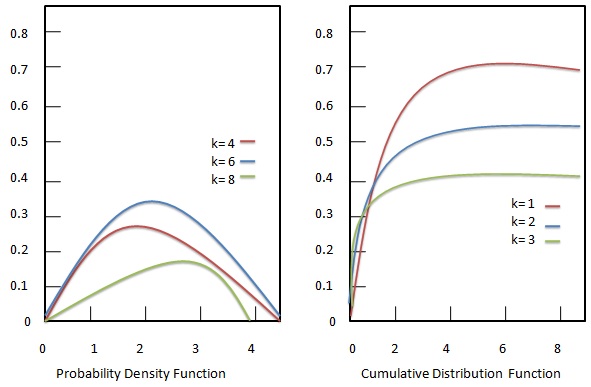
ฟังก์ชั่นความหนาแน่นของความน่าจะเป็น

ฟังก์ชันความหนาแน่นของความน่าจะเป็นของการแจกแจงแบบไคสแควร์ได้รับเป็น:

สูตร

$ {f (x; k) =} $ $ \ begin {cases} \ frac {x ^ {\ frac {k} {2} - 1} e ^ {- \ frac {x} {2}}} {2 ^ {\ frac {k} {2}} \ Gamma (\ frac {k} {2})}, & \ text {if $ x \ gt 0 $} \\ [7pt] 0, & \ text {ถ้า $ x \ le 0 $} \ end {cases} $

ที่ไหน -