Dalla fisica di Fermion

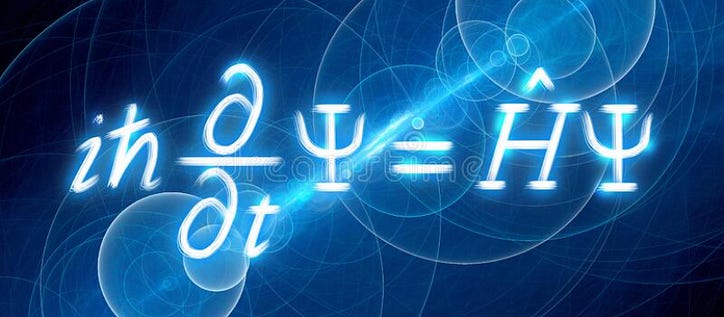
Se hai preso la fisica quantistica, o almeno ne hai sentito parlare, potresti aver sentito parlare di questo ragazzo di Schrodinger. Sai, quello con l'intera faccenda del gatto? Bene, è anche il tizio dietro una delle equazioni più utili della meccanica quantistica: l'equazione di Schròdinger. A prima vista, l'equazione può sembrare impossibile da risolvere (e in effetti in alcuni casi lo è!), ma dopo aver letto questo, capirai l'equazione e persino come risolverla per uno scenario. Pronto? Andiamo.

Ecco l'equazione. Sembra spaventoso: contiene persino dei forconi! Ma proviamo ad avere qualche intuizione su questa equazione. Inizieremo prima parlando dell'energia nella meccanica quantistica, promuovendola agli operatori, quindi parlando del ruolo della funzione d'onda. Dopodiché, uniremo tutto insieme e risolveremo l'equazione.

Meccanica Classica

Nella meccanica classica (e nella meccanica quantistica), la formula per l'energia è E = KE + PE dove E è l'energia totale, KE è l'energia cinetica e PE è l'energia potenziale. Ora KE e PE impiegano un po' di tempo a scrivere, quindi per risparmiare qualche millisecondo di scrittura, i fisici usano gli ovvi simboli di T e V per rappresentare rispettivamente l'energia cinetica e potenziale. Quindi ora abbiamo che E = T + V

Nota a piè di pagina: se hai preso la meccanica classica potresti notare che stiamo usando la formulazione hamiltoniana! Ci occuperemo della formulazione lagrangiana un altro giorno.

Ora sappiamo che T=p²/2m (formula per l'energia cinetica). Qui, m=massa, p=momento, e il simbolo più difficile di tutti, ½=metà. La massa è sempre costante, ma la quantità di moto non deve esserlo. Se qualcuno applica una forza a un oggetto, la quantità di moto inizierà a cambiare e si discosterà dal suo valore originale. Ora che dire dell'energia potenziale?

La formula per l'energia potenziale è V= -(integrale di F) dove F è la forza. Diventa evidente che l'energia potenziale dipende dalla forza applicata a un oggetto. In diversi scenari, la tua energia potenziale può assumere valori diversi poiché ci sono forze diverse. Ad esempio, in un pozzo gravitazionale il potenziale è V=mgx, ma in un oscillatore armonico il potenziale diventa V=(1/2)kx². Questo è molto importante perché risulta che i nostri "scenari" in cui risolviamo la nostra equazione di Schrodinger sono in realtà solo potenziali diversi. Questo avrà senso in seguito.

Prima quantizzazione

Ora, nella meccanica quantistica, prendiamo le nostre "osservabili" (T ed E) e facciamo loro avere un operatorecontroparti. Un operatore per i nostri scopi è solo una funzione che accetta un valore e ne emette un altro. Quindi T ha una controparte dell'operatore di energia cinetica, solitamente indicata con una T', e l'energia assume una controparte dell'operatore di energia, solitamente indicata con una H. L'energia potenziale è "data" invece che risolta, quindi non ha alcuna controparte dell'operatore. Ora l'operatore di energia cinetica è definito come un operatore dove quando agisce sulla funzione d'onda, restituisce l'energia cinetica della particella moltiplicata per la funzione d'onda. Stessa cosa con l'operatore Energia. Tutta questa faccenda potrebbe sembrare un po' inutile e astratta, ma fidati di me non lo è - ci stiamo arrivando. Ora ricorda come T=(1/2m)p²? Ciò implica che T' = (1/2m)p̂², dove p̂ è l' operatore momento . E come prima, p̂ ψ = p ψdove p è la quantità di moto della particella (di nuovo, un operatore agisce su una funzione e restituisce la funzione moltiplicata per qualunque valore sia correlato all'operatore). Ora si scopre che l'operatore quantità di moto è

p̂ = -ih(d/dx). Prendilo per scontato per ora. Questo implica che

T' = -h²/2m (d²/dx²). E poiché E = T + V, allora H=(-h²/2m)(d²/dx²) + V. Ora possiamo ora moltiplicare entrambi i lati per la funzione d'onda per ottenere

Hψ = -h²/2m (d²ψ/dx²) + Vψ

E ricorda da prima, H ψ = Eψ, quindi

E ψ = (-h²/2m)(d²ψ/dx²) + Vψ

Ora fai un respiro profondo. Abbiamo fatto molti calcoli e speriamo che tu non ti sia perso. Si scopre che abbiamo appena "derivato" l'equazione di Schrödinger! Ora, prima di parlare di come risolverlo, dobbiamo parlare di cosa sia questa "funzione d'onda".

Cos'è una funzione d'onda?

Nella meccanica classica, usiamo l'equazione hamiltoniana classica per risolvere le equazioni del moto per una particella. Le equazioni del moto sono solo le equazioni relative a dove si trova una particella in un dato momento nel tempo. Ad esempio, l'equazione del moto per una particella libera è x(t)=vt + x0. Possiamo trovare la posizione della particella per qualsiasi momento nel tempo se abbiamo la posizione iniziale e la velocità. Nella meccanica quantistica, usiamo invece l'equazione di Schrödinger per trovare qualcosa chiamato "funzione d'onda". La funzione d'onda stessa non è fisicamente significativa: non significa nulla e non ti dice nulla (direttamente). Ciò che è significativo è il quadrato della funzione d'onda che ti dà la densità di probabilità. La densità di probabilità è solo una funzione che ti dice la possibilità di trovare una particella in un certo intervallo quando la misuri. Quindi possiamo quindi dire che la funzione d'onda è solo la "radice quadrata" della densità di probabilità. Ora abbiamo finalmente tutte le conoscenze di base per parlare di cosa sia l'equazione di Schrodinger .

Come possiamo vedere dall'equazione precedente, tutto è costante tranne l'energia potenziale V(x). Prendiamo una particolare energia potenziale e risolviamo l'equazione per il caso in cui hai quella particolare energia potenziale. È così bello, perché non importa quali stress ci sono sul tuo sistema, o il calore, la carica, la tensione, lo chiami - non devi tenere conto di nulla di tutto ciò. Tutto quello che devi sapere è solo la funzione dell'energia potenziale e puoi risolvere l'equazione

(Se vogliamo essere pedanti qui, potremmo dire che "tecnicamente", stiamo incorporando tutte queste cose all'interno del potenziale stesso. Inoltre, la cosa del triangolo capovolto è l'abbreviazione di derivata seconda)

Calcolo

(se non ti piace il calcolo puoi saltare questa parte)

Ora, risolviamo l'equazione di Schrödinger per un potenziale semplice dove V(x)=0 ovunque. Questa è nota come particella libera, poiché le forze nette su di essa sono pari a zero. È libero da ogni oppressione! Nel caso classico, l'equazione del moto sarebbe x(t)=vt + x0 che forma una retta su un grafico spazio-temporale. Vediamo come appare la funzione d'onda per il caso quantistico.

Poiché V(x)=0, allora l'equazione di Schrodinger diventa

-h²/2m(d²ψ /dx²) = Eψ

Possiamo quindi riorganizzare e ottenere

d²ψ /dx² = -2mEψ/h²

Possiamo ora vedere che tutti i termini a destra sono costanti tranne ψ. Questo è un bene perché rende l'equazione facile da risolvere. Possiamo quindi definire una costante k come sqrt(2mE/h), il che significa che ora abbiamo

d²ψ / dx² = -k²ψ

Quindi aggiungiamo entrambi i lati dell'equazione per il termine della mano destra

d²ψ/dx² + k²ψ = 0

Assumiamo quindi che ψ(x) = exp(rx)

e da questo otteniamo

r=-k², r= +ik o -ik

Ciò significa che ψ( x)=exp(ikx) o

ψ( x)=exp(-ikx)

Poiché l'equazione è lineare, possiamo prendere una sovrapposizione (combinazione lineare) di entrambe le parti per ottenere la soluzione generale

ψ(x) = Aexp(ikx) + Bexp(-ikx)

e tecnicamente abbiamo finito. Forse ti starai chiedendo come possiamo persino determinare le costanti A e B. Di solito lo faremmo con qualcosa chiamato normalizzazione, ma questa è una storia per un'altra volta. Si scopre che per questo scenario non può essere normalizzato. Questo è un linguaggio stravagante per la funzione d'onda che non si avvicina allo zero mentre vai all'infinito o meno all'infinito. Quindi per quali valori A e B corrispondono a questo stato? Bene, si scopre che questo non è in realtà uno stato possibile poiché non puoi normalizzarlo. Ops!

Non preoccuparti però! Si scopre che una sovrapposizione di tutte le possibili funzioni d'onda può produrre uno stato reale. Questo porta molte cose interessanti di per sé, ma anche questa è una storia per la prossima volta.

Grazie per aver letto! Questo sito Web fa un pessimo lavoro nella formattazione dei simboli matematici, quindi parte del testo matematico non veniva visualizzato correttamente. Se vuoi vedere una derivazione video della stessa cosa, ho realizzato un video qui sul mio canale Fermion Physics sulla soluzione (anche se parlo abbastanza velocemente). Il passaggio dal video a questo articolo contribuirà a rendere più chiara la soluzione. Fino alla prossima volta!