โดยเฟอร์มิออนฟิสิกส์

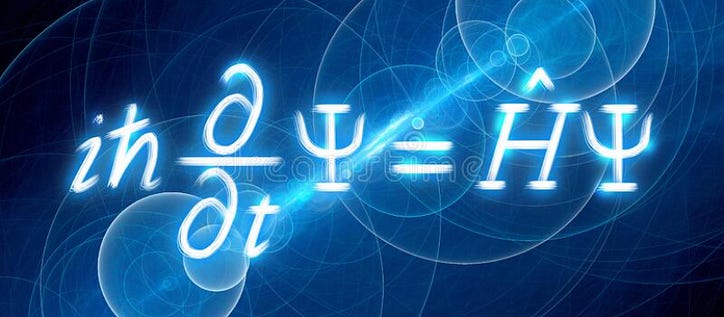
ถ้าคุณเคยเรียนฟิสิกส์ควอนตัม หรืออย่างน้อยก็เคยได้ยินเรื่องนี้มาก่อน คุณอาจเคยได้ยินชื่อชเรอดิงเงอร์คนนี้ คุณรู้ไหม - คนที่มีแมวทั้งตัว? เขายังเป็นผู้อยู่เบื้องหลังหนึ่งในสมการที่มีประโยชน์ที่สุดในกลศาสตร์ควอนตัม นั่นคือสมการชเรอดิงเงอร์ เมื่อดูครั้งแรก สมการอาจดูเหมือนแก้ไม่ได้ (และในบางกรณีก็แก้ได้!) แต่หลังจากอ่านบทความนี้แล้ว คุณจะเข้าใจสมการและแม้กระทั่งวิธีแก้สมการสำหรับสถานการณ์หนึ่งๆ พร้อม? ไปกันเถอะ.

นี่คือสมการ มันดูน่ากลัว มันยังมีโกยอยู่ในนั้นด้วย! แต่ลองมาทำความเข้าใจสมการนี้กัน อันดับแรก เราจะเริ่มด้วยการพูดถึงพลังงานในกลศาสตร์ควอนตัม นำเสนอแก่ผู้ดำเนินการ จากนั้นจึงพูดถึงบทบาทของฟังก์ชันคลื่น หลังจากนั้นเราจะต่อทุกอย่างเข้าด้วยกันและแก้สมการ

กลศาสตร์คลาสสิค

ในกลศาสตร์คลาสสิก (และกลศาสตร์ควอนตัม) สูตรของพลังงานคือ E = KE + PE โดยที่Eคือพลังงานทั้งหมดKEคือพลังงานจลน์ และ PE คือพลังงานศักย์ ตอนนี้ KE และ PE ใช้เวลาเขียนค่อนข้างนาน ดังนั้นเพื่อประหยัดเวลาในการเขียนไม่กี่มิลลิวินาที นักฟิสิกส์จึงใช้สัญลักษณ์ที่ชัดเจนของ T และ V เพื่อแสดงถึงพลังงานจลน์และพลังงานศักย์ตามลำดับ ตอนนี้เราได้ว่า E = T + V

เชิงอรรถ: หากคุณเคยศึกษากลไกแบบคลาสสิก คุณอาจสังเกตเห็นว่าเรากำลังใช้สูตรของแฮมิลตัน! เราจะจัดการกับสูตร Lagrangian ในวันอื่น

ตอนนี้เรารู้แล้วว่า T=p²/2m (สูตรสำหรับพลังงานจลน์) ในที่นี้ m=มวล, p=โมเมนตัม และสัญลักษณ์ที่ยากที่สุดคือ ½=ครึ่ง มวลคงที่เสมอ แต่โมเมนตัมไม่จำเป็นต้องคงที่ ถ้ามีคนออกแรงกระทำต่อวัตถุ โมเมนตัมจะเริ่มเปลี่ยนแปลงและเบี่ยงเบนไปจากค่าเดิม แล้วพลังงานศักย์ล่ะ?

สูตรสำหรับพลังงานศักย์คือ V= -(อินทิกรัลของ F) โดยที่ F คือแรง เห็นได้ชัดว่าพลังงานศักย์ขึ้นอยู่กับแรงที่กระทำต่อวัตถุ ในสถานการณ์ที่แตกต่างกัน พลังงานศักย์ของคุณสามารถมีค่าต่างกันได้เนื่องจากมีแรงต่างกัน ตัวอย่างเช่น ในหลุมแรงโน้มถ่วง ศักย์คือ V=mgx แต่ในฮาร์มอนิกออสซิลเลเตอร์ ศักย์จะกลายเป็น V=(1/2)kx² สิ่งนี้สำคัญมากเพราะกลายเป็นว่า "สถานการณ์" ที่เราแก้สมการชเรอดิงเงอร์นั้นมีศักยภาพที่แตกต่างกันจริงๆ สิ่งนี้จะสมเหตุสมผลในภายหลัง

การวัดปริมาณครั้งแรก

ตอนนี้ในกลศาสตร์ควอนตัม เราใช้ "สิ่งที่สังเกตได้" (T และ E) และทำให้พวกมันมีโอเปอเรเตอร์คู่ ตัวดำเนินการสำหรับวัตถุประสงค์ของเราเป็นเพียงฟังก์ชันที่รับค่าหนึ่งและแยกค่าอื่นออกมา ดังนั้น T จึงมีตัวดำเนินการพลังงานจลน์ซึ่งมักจะเขียนแทนด้วย T' และพลังงานที่ใช้กับตัวดำเนินการพลังงานมักจะเขียนแทนด้วย H พลังงานศักย์ถูก "ให้" แทนที่จะแก้ไขได้ ดังนั้นจึงไม่มี คู่ดำเนินการ ตอนนี้ตัวดำเนินการพลังงานจลน์ถูกกำหนดให้เป็นตัวดำเนินการซึ่งเมื่อทำหน้าที่ในฟังก์ชันคลื่น มันจะส่งกลับพลังงานจลน์ของอนุภาคคูณด้วยฟังก์ชันคลื่น สิ่งเดียวกันกับผู้ประกอบการด้านพลังงาน สิ่งทั้งหมดนี้อาจดูไร้ประโยชน์และเป็นนามธรรมเล็กน้อย แต่เชื่อฉันเถอะว่าไม่ใช่ - เรากำลังไปถึงจุดนั้น ทีนี้จำได้ไหมว่า T=(1/2m)p²? นี่หมายความว่า T' = (1/2m)p̂² โดยที่ p̂ คือโอเปอเรเตอร์โมเมนตัม และเช่นเคย p̂ ψ = p ψโดยที่ p คือโมเมนตัมของอนุภาค (อีกครั้ง ตัวดำเนินการทำหน้าที่ในฟังก์ชันและส่งกลับฟังก์ชันคูณด้วยค่าใดก็ตามที่เกี่ยวข้องกับตัวดำเนินการ) ตอนนี้ปรากฎว่าตัวดำเนินการโมเมนตัมคือ

p̂ = -ih(d/dx). ใช้เป็นที่กำหนดสำหรับตอนนี้ นี่หมายความว่า

T' = -h²/2m (d²/dx²) และเนื่องจาก E = T + V ดังนั้น H=(-h²/2m)(d²/dx²) + V ตอนนี้เราสามารถคูณทั้งสองข้างด้วยฟังก์ชันคลื่นเพื่อรับ

H ψ = -h²/2m (d²ψ/dx²) + Vψ

และจำไว้ก่อนหน้านี้ H ψ = Eψดังนั้น

E ψ = (-h²/2m)(d²ψ/dx²) + Vψ

ตอนนี้หายใจเข้าลึกๆ เราทำคณิตศาสตร์มากมายและหวังว่าคุณจะไม่หลงทาง ปรากฎว่าเราเพิ่ง "ได้รับ" สมการชเรอดิงเงอร์! ตอนนี้ก่อนที่เราจะพูดถึงการแก้ปัญหา เราต้องพูดถึงว่า "ฟังก์ชันคลื่น" นี้คืออะไร

ฟังก์ชันคลื่นคืออะไร?

ในกลศาสตร์คลาสสิก เราใช้สมการแฮมิลตันแบบดั้งเดิมในการแก้สมการการเคลื่อนที่ของอนุภาค สมการการเคลื่อนที่เป็นเพียงสมการของตำแหน่งที่อนุภาคอยู่ในช่วงเวลาที่กำหนด ตัวอย่างเช่น สมการการเคลื่อนที่ของอนุภาคอิสระคือ x(t)=vt + x0 เราสามารถหาตำแหน่งของอนุภาคในช่วงเวลาใดก็ได้ถ้าเรามีตำแหน่งเริ่มต้นและความเร็ว ในกลศาสตร์ควอนตัม เราใช้สมการชเรอดิงเงอร์เพื่อค้นหาสิ่งที่เรียกว่า "ฟังก์ชันคลื่น" แทน ฟังก์ชันคลื่นนั้นไม่ได้มีความหมายทางกายภาพ — มันไม่ได้มีความหมายอะไรเลยและไม่ได้บอกอะไรคุณเลย (โดยตรง) สิ่งที่มีความหมายคือกำลังสองของฟังก์ชันคลื่นซึ่งให้ความหนาแน่นของความน่าจะ เป็นแก่คุณ. ความหนาแน่นของความน่าจะเป็นเป็นเพียงฟังก์ชันที่บอกโอกาสที่คุณพบอนุภาคในบางช่วงเมื่อคุณทำการวัด ดังนั้น เราสามารถพูดได้ว่าฟังก์ชันคลื่นเป็นเพียง "รากที่สอง" ของความหนาแน่นของความน่าจะเป็น ในที่สุดเราก็มีความรู้พื้นฐานทั้งหมดเพื่อพูดคุยเกี่ยวกับสมการชเรอดิงเงอร์

ดังที่เราเห็นได้จากสมการข้างต้น ทุกอย่างคงที่ ยกเว้นพลังงานศักย์ V(x) เราใช้พลังงานศักย์เฉพาะ และแก้สมการในกรณีที่คุณมีพลังงานศักย์นั้น สิ่งนี้สวยงามมาก เพราะไม่สำคัญว่าระบบของคุณจะมีความเครียดอะไร หรือความร้อน ประจุไฟฟ้า แรงดันไฟฟ้า คุณไม่ต้องคำนึงถึงสิ่งเหล่านี้ สิ่งที่คุณต้องรู้ก็แค่ฟังก์ชันพลังงานศักย์และคุณสามารถแก้สมการได้

(หากเราต้องการพูดอวดรู้ในที่นี้ เราอาจพูดได้ว่า "ในทางเทคนิค" เรากำลังรวมสิ่งเหล่านั้นทั้งหมดไว้ในศักยภาพของมันเอง นอกจากนี้ สิ่งที่สามเหลี่ยมกลับหัวยังสั้นสำหรับอนุพันธ์อันดับสอง)

การคำนวณ

(หากคุณไม่ชอบแคลคูลัส คุณสามารถข้ามส่วนนี้ได้)

ทีนี้ เรามาแก้สมการชเรอดิงเงอร์เพื่อหาศักย์ไฟฟ้าอย่างง่ายโดยที่ V(x)=0 ทุกที่ สิ่งนี้เรียกว่าอนุภาคอิสระ เนื่องจากแรงลัพธ์บนอนุภาคนั้นเป็นศูนย์ ปราศจากการกดขี่ทั้งปวง! ในกรณีคลาสสิก สมการการเคลื่อนที่จะเป็น x(t)=vt + x0 ซึ่งสร้างเส้นตรงบนกราฟปริภูมิ-เวลา มาดูกันว่าฟังก์ชันคลื่นมีลักษณะอย่างไรสำหรับกรณีควอนตัม

เนื่องจาก V(x)=0 สมการชเรอดิงเงอร์จะกลายเป็น

-h²/2m(d² ψ/dx²) = Eψ

จากนั้นเราสามารถจัดเรียงใหม่และรับได้

d² ψ/dx² = -2mEψ/h²

ตอนนี้เราจะเห็นว่าเงื่อนไขทั้งหมดทางด้านขวามือเป็นค่าคงที่ ยกเว้นψ นี่ เป็นสิ่งที่ดีเพราะมันทำให้แก้สมการได้ง่าย จากนั้นเราสามารถกำหนดค่าคงที่ k ให้เป็น sqrt(2mE/h) ซึ่งหมายความว่าตอนนี้เรามี

d²ψ / dx² = -k²ψ

จากนั้นเราก็บวกทั้งสองข้างของสมการด้วยเทอมขวามือ

d²ψ/dx² + k²ψ = 0

จากนั้นเราจะถือว่าψ(x) = exp(rx)

และจากนี้เราได้รับ

r=-k², r= +ik หรือ -ik

ซึ่งหมายความว่าψ( x)=exp(ikx) หรือ

ψ( x)=ประสบการณ์(-ikx)

เนื่องจากสมการเป็นเชิงเส้นเราจึงสามารถใช้การซ้อนทับ (การรวมกันเชิงเส้น) ของทั้งสองส่วนเพื่อให้ได้คำตอบทั่วไป

ψ(x) = Aexp(ikx) + Bexp(-ikx)

และเราเสร็จสิ้นทางเทคนิคแล้ว คุณอาจสงสัยว่าเราจะหาค่าคงที่ A และ B ได้อย่างไร โดยปกติแล้วเราจะทำสิ่งนี้โดยใช้สิ่งที่เรียกว่าNormalizationแต่นั่นก็เป็นเรื่องสำหรับเวลาอื่น ปรากฎว่าสำหรับสถานการณ์นี้ไม่สามารถทำให้เป็นมาตรฐานได้ นั่นเป็นภาษาแฟนซีสำหรับฟังก์ชันคลื่นที่ไม่เข้าใกล้ศูนย์เมื่อคุณไปที่ระยะอนันต์หรือลบระยะอนันต์ ดังนั้นสำหรับค่า A และ B ที่สอดคล้องกับสถานะนี้ ปรากฎว่านี่ไม่ใช่สถานะที่เป็นไปได้จริง ๆ เนื่องจากคุณไม่สามารถทำให้เป็นมาตรฐานได้ อ๊ะ!

ไม่ต้องกังวล! ปรากฎว่าการซ้อนทับของฟังก์ชันคลื่นที่เป็นไปได้ทั้งหมดสามารถทำให้เกิดสถานะจริงได้ สิ่งนี้นำมาซึ่งสิ่งดีๆ มากมายในตัวมันเอง — แต่นั่นก็เป็นเรื่องราวสำหรับครั้งหน้าเช่นกัน

ขอบคุณที่อ่าน! เว็บไซต์นี้จัดรูปแบบสัญลักษณ์ทางคณิตศาสตร์ได้แย่มาก ดังนั้นข้อความทางคณิตศาสตร์บางส่วนจึงแสดงผลได้ไม่ดีนัก หากคุณต้องการดูวิดีโอที่มาจากสิ่งเดียวกัน ฉันได้ทำวิดีโอที่นี่ในช่องFermion Physics ของฉันเกี่ยวกับการแก้ปัญหา (แม้ว่าฉันจะพูดค่อนข้างเร็วก็ตาม) การสลับไปมาระหว่างวิดีโอและบทความนี้จะช่วยให้การแก้ปัญหาชัดเจนยิ่งขึ้น ครั้งหน้า!