Czy można zastosować drzewo Sterna-Brocota, aby uzyskać lepszą zbieżność plików $2^m/3^n$?
Wymagane czytanie:
- Czy jakiekolwiek pozytywne rzeczywiste można przybliżyć jako $2^m/3^n$ z $(m,n)$ wystarczająco duży?
- Sekwencja drzewa rufowego Brocota
Powód, dla którego szukałem procedury, która nie ma tej wady, tj. W której następne przybliżenie jest zawsze bliższe pożądanemu rezultatowi. To jest to, czego do tej pory próbowałem.
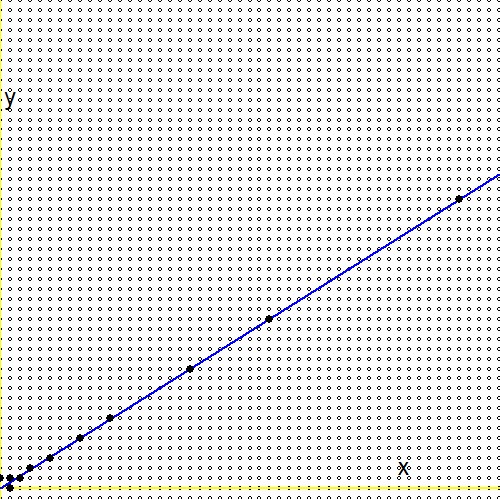
Zgodnie z pytaniem (2.), dla każdej dodatniej liczby rzeczywistej$0 \lt g \lt 1$istnieje nieskończona sekwencja w drzewie Sterna Brocota […], która zbiega się do liczby rzeczywistej. Tymczasem to pytanie ma odpowiedź , a jej główny wynik brzmi następująco: $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$ Mając na uwadze pytanie (1.), zastępujemy $\ln(2)/\ln(3)$ dla tego numeru $g$. Z tego wynika, że: $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$Można sobie wyobrazić przeszukiwanie drzewa Stern-Brocot. Niebieska linia to funkcja $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$, małe kółka to ułamki odwzorowane na siatce $\,m/n \to (m,n)\,$, masywnie czarne kropki to ułamki w drzewie Sterna-Brocota. Widać, że przeszukiwanie drzewa jest znacznie bardziej wydajne niż zwiększanie $m$ i $n$ z przyrostami pojedynczo.
Teraz porównaj wyrażenie w drugim wierszu powyższych wzorów z analogicznym wyrażeniem w odnośniku (1.): $$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$ I przygotuj się na rozczarowanie: logarytm arbitralnej rzeczywistości $r$brakuje! Lub alternatywnie:$\ln(r)=0$ lub $r=1$. Oznacza to, że nasze „nieskończone poszukiwanie” przez drzewo Sterna-Brocota, choć bardzo wydajne, ostatecznie prowadzi do przybliżenia tylko dla numeru jeden. Uważam to za dziwne, ponieważ - graficznie - nie wydaje się, aby między nimi była duża różnica$\color{red}{2^m/3^n \to r}$ i $\color{blue}{2^m/3^n \to 1}$:
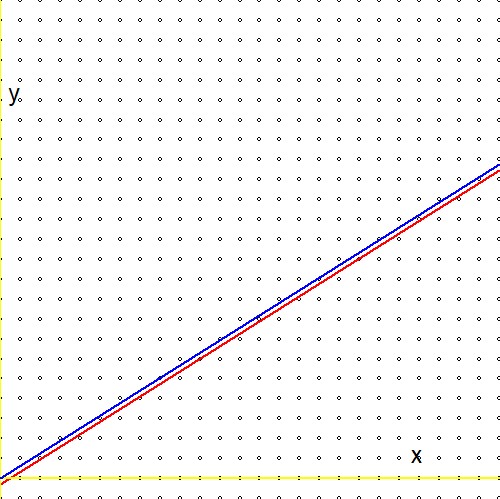
Stąd PYTANIE: czy istnieje sposób na dostosowanie procedury Sterna-Brocota tak, aby działała w innych sytuacjach?
EDYTOWAĆ.
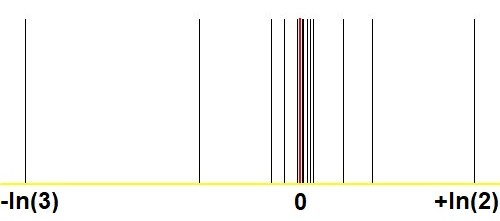
Oto kolejny wykres, który pokazuje zdumiewającą zbieżność z metodą Sterna-Brocota, w porównaniu z analogicznymi obrazami w moim pytaniu i odpowiedzi. Czy jakiekolwiek pozytywne rzeczywiste można przybliżyć jako$2^m/3^n$ z $(m,n)$wystarczająco duży? :
Odpowiedzi
Podam podejście, które nie wykorzystuje procedury Sterna-Brocota.
Wystarczy to pokazać $\frac{2^{m}}{3^{n}}$jest gęsty w przedziale [1,2]. Od czasu brania$\alpha\in (0,\infty)$ poza tym przedziałem jest ich trochę $k\in Z$ po to aby $\alpha = 2^{k}\gamma $ dla niektórych $\gamma \in [1,2]$. Wtedy wiemy, że jest sekwencja$\frac{2^{m}}{3^{n}}$ który się zbliża $\gamma$, mnożąc sekwencję termicznie przez $2^{k}$ (prawdopodobnie biorąc ogon sekwencji), otrzymujemy sekwencję w $\frac{2^{m}}{3^{n}}$ który się zbliża $\alpha$.
Następnie weź pod uwagę, że mapa $f:[1,2] -> [0,1]$ z $f(x) = log_{2}(x)$ jest bijekcją.
Obraz $\frac{2^{m}}{3^{n}}$ pod mapą jest $N-Nlog_{2}(3)$. Więc wystarczy to pokazać$N-Nlog_{2}(3)$ jest gęsty $[0,1]$.
Jest to konsekwencja twierdzenia Weyla o Equidistribution, które jest szczególnym przypadkiem twierdzenia ergodycznego.
Rozważać $a=2-log_{2}(3) = log_{2}(\frac{4}{3})$, więc $a$ jest na obrazie zestawu, tak jest $na = log_{2}(\frac{4^{n}}{3^{n}})$ i tak jest ułamkowa część $na$.
Twierdzenie Weyla Equidistribution (co nie jest trywialnym wynikiem) pokazuje, że dla nieracjonalnej części ułamkowej $na$jest równomiernie rozłożony, a zatem gęsty na [0,1]. Od$2-log_{2}(3)$ jest irracjonalne, możesz użyć tego twierdzenia.