Czy matematyka zmiennoprzecinkowa jest zepsuta?

Question

Rozważ następujący kod:

0.1 + 0.2 == 0.3  ->  false

0.1 + 0.2         ->  0.30000000000000004

Dlaczego zdarzają się te nieścisłości?

Answer 1

Binarna matematyka zmiennoprzecinkowa jest taka. W większości języków programowania jest oparty na standardzie IEEE 754 . Sedno problemu polega na tym, że liczby są przedstawiane w tym formacie jako liczba całkowita pomnożona przez potęgę dwójki; liczb wymiernych (takich jak 0.1, które jest 1/10), których mianownikiem nie jest potęga dwójki, nie można dokładnie przedstawić.

W 0.1standardowym binary64formacie reprezentacja może być zapisana dokładnie jako

• 0.1000000000000000055511151231257827021181583404541015625 dziesiętnie lub
• 0x1.999999999999ap-4w notacji hexfloat C99 .

Natomiast liczbę wymierną 0.1, którą jest 1/10, można zapisać dokładnie jako

• 0.1 dziesiętnie lub
• 0x1.99999999999999...p-4w analogicznej notacji hexfloat C99, gdzie ...reprezentuje niekończącą się sekwencję dziewiątek.

Stałe 0.2iw 0.3twoim programie będą również przybliżeniami do ich prawdziwych wartości. Zdarza się, że najbliżej doublecelu 0.2jest większa niż liczba racjonalnego 0.2ale że najbliżej doublecelu 0.3jest mniejsza niż liczba wymierna 0.3. Suma 0.1i 0.2kończy się tym, że jest większa niż liczba wymierna, 0.3a zatem nie zgadza się ze stałą w twoim kodzie.

Dość kompleksowe podejście do zagadnień arytmetyki zmiennoprzecinkowej jest tym, co każdy informatyk powinien wiedzieć o arytmetyce zmiennoprzecinkowej . Łatwiejsze do zrozumienia wyjaśnienie znajdziesz na stronie floating-point-gui.de .

Uwaga boczna: Wszystkie systemy liczb pozycyjnych (podstawa-N) dzielą ten problem z precyzją

Zwykłe stare liczby dziesiętne (podstawa 10) mają te same problemy, dlatego liczby takie jak 1/3 kończą się jako 0,333333333 ...

Właśnie natrafiłeś na liczbę (3/10), która jest łatwa do przedstawienia w systemie dziesiętnym, ale nie pasuje do systemu binarnego. Działa to również w obie strony (w pewnym stopniu): 1/16 to brzydka liczba dziesiętna (0,0625), ale w systemie dwójkowym wygląda tak dobrze, jak dziesiętna dziesiętna 10000 (0,0001) ** - gdybyśmy byli w zwyczaju używania systemu liczb o podstawie 2 w naszym codziennym życiu, spojrzałbyś nawet na tę liczbę i instynktownie zrozumiałeś, że możesz tam dotrzeć, dzieląc coś o połowę, zmniejszając o połowę raz za razem.

** Oczywiście nie jest to dokładnie sposób, w jaki liczby zmiennoprzecinkowe są przechowywane w pamięci (używają formy notacji naukowej). Jednak ilustruje to punkt, w którym błędy binarnej precyzji zmiennoprzecinkowej mają tendencję do pojawiania się, ponieważ liczby „rzeczywiste”, z którymi zwykle jesteśmy zainteresowani, to często potęgi dziesiątek - ale tylko dlatego, że używamy systemu liczb dziesiętnych dzień- dzisiaj. Dlatego też powiemy na przykład 71% zamiast „5 na 7” (71% jest przybliżeniem, ponieważ 5/7 nie może być reprezentowane dokładnie przez żadną liczbę dziesiętną).

Więc nie: binarne liczby zmiennoprzecinkowe nie są zepsute, po prostu są tak niedoskonałe, jak każdy inny system liczbowy o podstawie N :)

Uwaga boczna: Praca z pływakami w programowaniu

W praktyce ten problem precyzji oznacza, że ​​przed ich wyświetleniem musisz użyć funkcji zaokrąglania, aby zaokrąglić liczby zmiennoprzecinkowe do dowolnej liczby miejsc po przecinku.

Musisz także zastąpić testy równości porównaniami, które pozwalają na pewną tolerancję, co oznacza:

Czy nie robićif (x == y) { ... }

Zamiast tego zrób if (abs(x - y) < myToleranceValue) { ... }.

gdzie absjest wartością bezwzględną. myToleranceValuemusi być wybrany dla twojej konkretnej aplikacji - i będzie to miało dużo wspólnego z tym, na ile "miejsca wiggle room" jesteś przygotowany na pozwolenie i jaka może być największa liczba, którą będziesz porównywać (ze względu na utratę problemów z precyzją ). Uważaj na stałe stylu „epsilon” w wybranym języku. Są to nie należy traktować jako wartości tolerancji.

Answer 2

Perspektywa projektanta sprzętu

Uważam, że powinienem dodać do tego perspektywę projektanta sprzętu, ponieważ projektuję i buduję sprzęt zmiennoprzecinkowy. Znajomość źródła błędu może pomóc w zrozumieniu tego, co dzieje się w oprogramowaniu, i ostatecznie mam nadzieję, że pomoże to wyjaśnić powody, dla których błędy zmiennoprzecinkowe zdarzają się i wydają się narastać w czasie.

1. Przegląd

Z punktu widzenia inżynierii większość operacji zmiennoprzecinkowych będzie zawierała pewien element błędu, ponieważ sprzęt wykonujący obliczenia zmiennoprzecinkowe musi mieć błąd mniejszy niż połowa jednej jednostki na ostatnim miejscu. Dlatego większość sprzętu zatrzyma się z precyzją niezbędną tylko do uzyskania błędu mniejszego niż połowa jednej jednostki na ostatnim miejscu dla pojedynczej operacji, co jest szczególnie problematyczne w przypadku dzielenia zmiennoprzecinkowego. To, co stanowi pojedynczą operację, zależy od tego, ile operandów przyjmuje jednostka. W większości są to dwa, ale niektóre jednostki przyjmują 3 lub więcej operandów. Z tego powodu nie ma gwarancji, że powtarzające się operacje spowodują pożądany błąd, ponieważ błędy sumują się w czasie.

2. Normy

Większość procesorów jest zgodna ze standardem IEEE-754, ale niektóre używają zdenormalizowanych lub innych standardów. Na przykład w IEEE-754 istnieje tryb zdenormalizowany, który umożliwia reprezentację bardzo małych liczb zmiennoprzecinkowych kosztem precyzji. Poniższe informacje dotyczą jednak znormalizowanego trybu IEEE-754, który jest typowym trybem działania.

W standardzie IEEE-754 projektanci sprzętu mogą mieć dowolną wartość błędu / epsilon, o ile jest mniejsza niż połowa jednej jednostki na ostatnim miejscu, a wynik musi być mniejszy niż połowa jednej jednostki w ostatnim miejscu miejsce na jedną operację. To wyjaśnia, dlaczego w przypadku powtarzających się operacji błędy sumują się. W przypadku podwójnej precyzji IEEE-754 jest to 54-ty bit, ponieważ 53 bity są używane do reprezentowania części numerycznej (znormalizowanej), zwanej także mantysą, liczby zmiennoprzecinkowej (np. 5.3 w 5.3e5). W następnych sekcjach bardziej szczegółowo opisano przyczyny błędów sprzętowych w różnych operacjach zmiennoprzecinkowych.

3. Przyczyna błędu zaokrągleń w dzieleniu

Główną przyczyną błędu w dzieleniu zmiennoprzecinkowym są algorytmy dzielenia użyte do obliczenia ilorazu. Większość systemów komputerowych obliczyć podział stosując mnożenie przez odwrotność, głównie w Z=X/Y, Z = X * (1/Y). Dzielenie jest obliczane iteracyjnie, tj. Każdy cykl oblicza niektóre bity ilorazu, aż do osiągnięcia pożądanej precyzji, co dla IEEE-754 jest czymś z błędem mniejszym niż jedna jednostka na ostatnim miejscu. Tablica odwrotności Y (1 / Y) jest znana jako tablica wyboru ilorazu (QST) w powolnym dzieleniu, a rozmiar w bitach tablicy wyboru ilorazu to zwykle szerokość podstawy lub liczba bitów iloraz obliczany w każdej iteracji plus kilka bitów ochronnych. W przypadku standardu IEEE-754 podwójnej precyzji (64-bitowy) byłby to rozmiar podstawy dzielnika plus kilka bitów ochronnych k, gdzie k>=2. Na przykład typowa tabela doboru ilorazów dla dzielnika, który oblicza 2 bity ilorazu naraz (podstawa 4) to 2+2= 4bity (plus kilka opcjonalnych bitów).

3.1 Błąd zaokrąglania działek: przybliżenie wzajemności

To, jakie odwrotności znajdują się w tabeli doboru ilorazów, zależy od metody dzielenia : powolny podział, taki jak podział SRT, lub szybki podział, taki jak podział Goldschmidta; każdy wpis jest modyfikowany zgodnie z algorytmem dzielenia w celu uzyskania najmniejszego możliwego błędu. W każdym razie jednak wszystkie odwrotności są przybliżeniami rzeczywistej odwrotności i wprowadzają pewien element błędu. Zarówno metoda wolnego dzielenia, jak i szybkiego dzielenia obliczają iloraz iteracyjnie, tj. W każdym kroku obliczana jest pewna liczba bitów ilorazu, następnie wynik jest odejmowany od dywidendy, a dzielnik powtarza kroki, aż błąd będzie mniejszy niż połowa jedności jednostka na ostatnim miejscu. Metody powolnego podziału obliczają stałą liczbę cyfr ilorazu w każdym kroku i są zwykle tańsze w budowie, a metody szybkiego dzielenia obliczają zmienną liczbę cyfr na krok i są zwykle droższe w budowie. Najważniejszą częścią metod dzielenia jest to, że większość z nich polega na wielokrotnym mnożeniu przez przybliżenie odwrotności, więc są podatne na błędy.

4. Zaokrąglanie błędów w innych operacjach: obcięcie

Inną przyczyną błędów zaokrąglania we wszystkich operacjach są różne tryby obcinania ostatecznej odpowiedzi, na które pozwala IEEE-754. Są obcięte, zaokrąglone do zera, zaokrąglone do najbliższej (domyślnie), zaokrąglone w dół i zaokrąglone w górę. Wszystkie metody wprowadzają element błędu mniejszy niż jedna jednostka na ostatnim miejscu dla pojedynczej operacji. Z biegiem czasu i powtarzającymi się operacjami obcięcie również kumuluje się z wynikowym błędem. Ten błąd obcięcia jest szczególnie problematyczny przy potęgowaniu, które wiąże się z pewną formą wielokrotnego mnożenia.

5. Powtarzane operacje

Ponieważ sprzęt, który wykonuje obliczenia zmiennoprzecinkowe, musi dawać wynik z błędem mniejszym niż połowa jednej jednostki na ostatnim miejscu dla pojedynczej operacji, błąd będzie narastał w przypadku powtarzających się operacji, jeśli nie będzie obserwowany. To jest powód, dla którego w obliczeniach, które wymagają błędu ograniczonego, matematycy używają takich metod, jak użycie zaokrąglonej do najbliższej parzystej cyfry na ostatnim miejscu IEEE-754, ponieważ z biegiem czasu błędy są bardziej skłonne do wzajemnego znoszenia się. out i Interval Arithmetic w połączeniu z odmianami trybów zaokrąglania IEEE 754 w celu przewidywania błędów zaokrąglania i ich korygowania. Ze względu na niski względny błąd w porównaniu z innymi trybami zaokrąglania, zaokrąglenie do najbliższej parzystej cyfry (na ostatnim miejscu) jest domyślnym trybem zaokrąglania IEEE-754.

Zauważ, że domyślny tryb zaokrąglania, zaokrąglanie do najbliższej parzystej cyfry na ostatnim miejscu , gwarantuje błąd mniejszy niż połowa jednej jednostki na ostatnim miejscu dla jednej operacji. Użycie samego obcięcia, zaokrąglenia w górę i zaokrąglenia w dół może spowodować błąd większy niż połowa jednej jednostki na ostatnim miejscu, ale mniej niż jedną jednostkę na ostatnim miejscu, więc te tryby nie są zalecane, chyba że są używane w arytmetyce przedziałów.

6. Podsumowanie

Krótko mówiąc, podstawową przyczyną błędów w operacjach zmiennoprzecinkowych jest połączenie obcinania sprzętu i obcinania odwrotności w przypadku dzielenia. Ponieważ standard IEEE-754 wymaga tylko błędu mniejszego niż połowa jednej jednostki w ostatnim miejscu dla pojedynczej operacji, błędy zmiennoprzecinkowe w powtarzających się operacjach sumują się, chyba że zostaną poprawione.

Answer 3

Jest łamany dokładnie w taki sam sposób, jak zapis dziesiętny (podstawa-10) jest łamany, tylko dla podstawy-2.

Aby to zrozumieć, pomyśl o przedstawieniu 1/3 jako wartości dziesiętnej. Nie da się tego zrobić dokładnie! W ten sam sposób 1/10 (dziesiętna 0,1) nie może być reprezentowana dokładnie w podstawie 2 (binarnie) jako wartość „dziesiętna”; powtarzający się wzór po przecinku trwa w nieskończoność. Wartość nie jest dokładna i dlatego nie można na niej wykonywać dokładnych obliczeń przy użyciu zwykłych metod zmiennoprzecinkowych.

Answer 4

Większość odpowiedzi tutaj odnosi się do tego pytania w bardzo suchych, technicznych terminach. Chciałbym odnieść się do tego w kategoriach zrozumiałych dla normalnych ludzi.

Wyobraź sobie, że próbujesz pokroić pizzę. Masz zautomatyzowany nóż do pizzy, który może pokroić plasterki pizzy dokładnie na pół. Może przekroić o połowę całą pizzę lub podzielić istniejący kawałek na pół, ale w każdym przypadku dzielenie na pół jest zawsze dokładne.

Ta krajalnica do pizzy ma bardzo delikatne ruchy, a jeśli zaczniesz od całej pizzy, przekrój ją na pół i za każdym razem kontynuuj dzielenie na pół najmniejszego kawałka, możesz zrobić połowę 53 razy, zanim kawałek będzie za mały nawet dla jego wysoce precyzyjnych zdolności . W tym momencie nie możesz już przekroić na pół tego bardzo cienkiego plasterka, ale musisz go uwzględnić lub wykluczyć w takiej postaci, w jakiej jest.

A teraz, jak pokroiłbyś wszystkie plasterki w taki sposób, aby stanowiły jedną dziesiątą (0,1) lub jedną piątą (0,2) pizzy? Naprawdę o tym pomyśl i spróbuj to rozwiązać. Możesz nawet spróbować użyć prawdziwej pizzy, jeśli masz pod ręką mityczny, precyzyjny nóż do pizzy. :-)

---

Oczywiście większość doświadczonych programistów zna prawdziwą odpowiedź, która jest taka, że ​​nie ma sposobu, aby poskładać dokładnie dziesiątą lub piątą część pizzy przy użyciu tych plasterków, bez względu na to, jak dokładnie je pokroisz. Możesz zrobić całkiem niezłe przybliżenie i jeśli dodasz przybliżenie 0,1 do przybliżenia 0,2, otrzymasz całkiem niezłe przybliżenie 0,3, ale nadal jest to tylko przybliżenie.

W przypadku liczb o podwójnej precyzji (czyli dokładności, która pozwala na 53-krotne zmniejszenie o połowę pizzy), liczby natychmiast mniejsze i większe od 0,1 to 0,09999999999999999167332731531132594682276248931884765625 i 0,1000000000000000055511151231257827021181583404541015625. Ta ostatnia jest nieco bliższa 0,1 niż pierwsza, więc parser numeryczny, biorąc pod uwagę wartość wejściową 0,1, faworyzuje to drugie.

(Różnica między tymi dwiema liczbami to „najmniejszy wycinek”, który musimy uwzględnić albo uwzględnić, co wprowadza odchylenie w górę, albo wykluczyć, co wprowadza odchylenie w dół. Technicznym terminem określającym ten najmniejszy wycinek jest ulp .)

W przypadku 0,2 wszystkie liczby są takie same, po prostu przeskalowane o współczynnik 2. Ponownie preferujemy wartość, która jest nieco wyższa niż 0,2.

Zauważ, że w obu przypadkach przybliżenia dla 0,1 i 0,2 mają niewielkie odchylenie w górę. Jeśli dodamy wystarczająco dużo tych odchyleń, będą one przesuwać liczbę coraz dalej od tego, czego chcemy, i faktycznie, w przypadku 0,1 + 0,2 odchylenie jest na tyle duże, że wynikowa liczba nie jest już najbliższą liczbą do 0,3.

W szczególności, 0,1 + 0,2 to naprawdę 0,1000000000000000055511151231257827021181583404541015625 + 0.200000000000000011102230246251565404236316680908203125 = 0,300000000000000044408920985006261616945266329759936128759936132975993613289999361

---

PS Niektóre języki programowania zapewniają również krajalnice do pizzy, które mogą dzielić plasterki na dokładne dziesiąte części . Chociaż takie krajalnice do pizzy są rzadkością, jeśli masz do nich dostęp, powinieneś ich używać, gdy ważne jest, aby móc uzyskać dokładnie jedną dziesiątą lub jedną piątą kawałka.

(Pierwotnie opublikowane na Quora.)

Answer 5

Błędy zaokrągleń zmiennoprzecinkowych. 0,1 nie można przedstawić tak dokładnie w systemie o podstawie 2, jak w przypadku podstawy 10 z powodu braku czynnika pierwszego o wartości 5. Tak jak w przypadku 1/3 liczby dziesiętnej reprezentacji liczby cyfr jest liczba dziesiętna, ale w przypadku liczby dziesiętnej 3 wynosi "0,1", 0.1 przyjmuje nieskończoną liczbę cyfr o podstawie-2, podczas gdy nie ma podstawy-10. A komputery nie mają nieskończonej ilości pamięci.

Answer 6

Oprócz innych poprawnych odpowiedzi możesz rozważyć skalowanie wartości, aby uniknąć problemów z arytmetyką zmiennoprzecinkową.

Na przykład:

var result = 1.0 + 2.0;     // result === 3.0 returns true

... zamiast:

var result = 0.1 + 0.2;     // result === 0.3 returns false

Wyrażenie 0.1 + 0.2 === 0.3zwraca falsew JavaScript, ale na szczęście arytmetyka liczb całkowitych w zmiennoprzecinkowym jest dokładna, więc można uniknąć błędów w reprezentacji dziesiętnej poprzez skalowanie.

Jako praktyczny przykład, aby uniknąć problemów zmiennoprzecinkowych gdzie dokładność jest najważniejsza, zaleca się ¹ obchodzić się z pieniędzmi jako liczba całkowita reprezentująca liczbę centów: 2550centy zamiast 25.50dolarów.

---

¹ Douglas Crockford: JavaScript: Dobre części : Dodatek A - Okropne części (strona 105) .

Answer 7

Moja odpowiedź jest dość długa, więc podzieliłem ją na trzy części. Ponieważ pytanie dotyczy matematyki zmiennoprzecinkowej, położyłem nacisk na to, co faktycznie robi maszyna. Podałem również, że jest to specyficzne dla podwójnej (64-bitowej) precyzji, ale argument ma zastosowanie w równym stopniu do każdej arytmetyki zmiennoprzecinkowej.

Preambuła

Liczba w formacie binarnym zmiennoprzecinkowym o podwójnej precyzji IEEE 754 (binary64) reprezentuje liczbę w postaci

wartość = (-1) ^ s * (1 m ₅₁ m ₅₀ ... m ₂ m ₁ m ₀ ) ₂ * 2 ^e-1023

w 64 bitach:

• Pierwszy bit to bit znaku : 1jeśli liczba jest ujemna, w 0przeciwnym razie ¹ .
• Kolejnych 11 bitów to wykładnik , który jest przesunięty o 1023. Innymi słowy, po odczytaniu bitów wykładnika z liczby o podwójnej precyzji, 1023 musi zostać odjęte, aby otrzymać potęgę dwójki.
• Pozostałych 52 bitów z mantysy (lub mantysę). W mantysie „domniemany” 1.jest zawsze pomijany ^2, ponieważ najbardziej znaczący bit każdej wartości binarnej to 1.

¹ - IEEE 754 dopuszcza koncepcję zera ze znakiem - +0i -0są traktowane inaczej: 1 / (+0)jest dodatnią nieskończonością; 1 / (-0)jest nieskończonością ujemną. Dla wartości zerowych wszystkie bity mantysy i wykładnika wynoszą zero. Uwaga: wartości zerowe (+0 i -0) jawnie nie są klasyfikowane jako denormalne ² .

² - Nie dotyczy to liczb denormalnych , które mają przesunięty wykładnik równy zero (i domniemany 0.). Zakres normalnych liczb podwójnej precyzji to d _min ≤ | x | ≤ d _max , gdzie d _min (najmniejsza reprezentowalna liczba niezerowa) wynosi 2 ^{-1023 - 51} (≈ 4,94 * ^10-324 ) i d _max (największa liczba denormalna, dla której mantysa składa się wyłącznie z 1s) wynosi 2 ^{-1023 + 1} - 2 ^{-1023 - 51} (≈ 2.225 * 10 ^-308 ).

---

Zamiana liczby podwójnej precyzji na binarną

Istnieje wiele konwerterów online, które konwertują liczbę zmiennoprzecinkową o podwójnej precyzji na binarną (np. Na binaryconvert.com ), ale oto przykładowy kod C # do uzyskania reprezentacji IEEE 754 dla liczby o podwójnej precyzji (oddzielam trzy części dwukropkami ( :) :

public static string BinaryRepresentation(double value)
{
    long valueInLongType = BitConverter.DoubleToInt64Bits(value);
    string bits = Convert.ToString(valueInLongType, 2);
    string leadingZeros = new string('0', 64 - bits.Length);
    string binaryRepresentation = leadingZeros + bits;

    string sign = binaryRepresentation[0].ToString();
    string exponent = binaryRepresentation.Substring(1, 11);
    string mantissa = binaryRepresentation.Substring(12);

    return string.Format("{0}:{1}:{2}", sign, exponent, mantissa);
}

---

Przechodząc do sedna: pierwotne pytanie

(Przejdź do końca w przypadku wersji TL; DR)

Cato Johnston (zadający pytanie) zapytał, dlaczego 0,1 + 0,2! = 0,3.

Zapisane w systemie binarnym (z dwukropkami oddzielającymi trzy części), reprezentacje wartości IEEE 754 to:

0.1 => 0:01111111011:1001100110011001100110011001100110011001100110011010
0.2 => 0:01111111100:1001100110011001100110011001100110011001100110011010

Zauważ, że mantysa składa się z powtarzających się cyfr 0011. To jest kluczem do tego, dlaczego w obliczeniach występuje jakikolwiek błąd - 0,1, 0,2 i 0,3 nie mogą być reprezentowane binarnie dokładnie w skończonej liczbie bitów binarnych, a więcej niż 1/9, 1/3 lub 1/7 można przedstawić dokładnie w cyfry dziesiętne .

Zauważ również, że możemy zmniejszyć potęgę wykładnika o 52 i przesunąć punkt w reprezentacji binarnej w prawo o 52 miejsca (podobnie jak ^10-3 * 1,23 == ^10-5 * 123). Dzięki temu możemy przedstawić reprezentację binarną jako dokładną wartość, którą reprezentuje w postaci a * 2 ^p . gdzie „a” jest liczbą całkowitą.

Zamiana wykładników na dziesiętne, usunięcie przesunięcia i ponowne dodanie domniemanych 1(w nawiasach kwadratowych) wartości 0,1 i 0,2 to:

0.1 => 2^-4 * [1].1001100110011001100110011001100110011001100110011010
0.2 => 2^-3 * [1].1001100110011001100110011001100110011001100110011010
or
0.1 => 2^-56 * 7205759403792794 = 0.1000000000000000055511151231257827021181583404541015625
0.2 => 2^-55 * 7205759403792794 = 0.200000000000000011102230246251565404236316680908203125

Aby dodać dwie liczby, wykładnik musi być taki sam, czyli:

0.1 => 2^-3 *  0.1100110011001100110011001100110011001100110011001101(0)
0.2 => 2^-3 *  1.1001100110011001100110011001100110011001100110011010
sum =  2^-3 * 10.0110011001100110011001100110011001100110011001100111
or
0.1 => 2^-55 * 3602879701896397  = 0.1000000000000000055511151231257827021181583404541015625
0.2 => 2^-55 * 7205759403792794  = 0.200000000000000011102230246251565404236316680908203125
sum =  2^-55 * 10808639105689191 = 0.3000000000000000166533453693773481063544750213623046875

Ponieważ suma nie ma postaci 2 ⁿ * 1. {bbb} zwiększamy wykładnik o jeden i przesuwamy punkt dziesiętny ( binarny ), aby otrzymać:

sum = 2^-2  * 1.0011001100110011001100110011001100110011001100110011(1)
    = 2^-54 * 5404319552844595.5 = 0.3000000000000000166533453693773481063544750213623046875

Mantysa zawiera teraz 53 bity (53-ty jest w nawiasach kwadratowych w linii powyżej). Domyślnym trybem zaokrąglania dla IEEE 754 jest „ Round to Nearest ” - tj. Jeśli liczba x mieści się między dwiema wartościami a i b , wybierana jest wartość, w której najmniej znaczący bit wynosi zero.

a = 2^-54 * 5404319552844595 = 0.299999999999999988897769753748434595763683319091796875
  = 2^-2  * 1.0011001100110011001100110011001100110011001100110011

x = 2^-2  * 1.0011001100110011001100110011001100110011001100110011(1)

b = 2^-2  * 1.0011001100110011001100110011001100110011001100110100
  = 2^-54 * 5404319552844596 = 0.3000000000000000444089209850062616169452667236328125

Zauważ, że a i b różnią się tylko ostatnim bitem; ...0011+ 1= ...0100. W tym przypadku wartością z najmniej znaczącym bitem zerowym jest b , więc suma wynosi:

sum = 2^-2  * 1.0011001100110011001100110011001100110011001100110100
    = 2^-54 * 5404319552844596 = 0.3000000000000000444089209850062616169452667236328125

podczas gdy binarna reprezentacja 0,3 to:

0.3 => 2^-2  * 1.0011001100110011001100110011001100110011001100110011
    =  2^-54 * 5404319552844595 = 0.299999999999999988897769753748434595763683319091796875

która różni się tylko od binarnej reprezentacji sumy 0,1 i 0,2 przez ^2-54 .

Binarne reprezentacje 0,1 i 0,2 są najdokładniejszymi reprezentacjami liczb dopuszczalnych przez IEEE 754. Dodanie tych reprezentacji, ze względu na domyślny tryb zaokrąglania, daje w wyniku wartość, która różni się tylko najmniej znaczącym bitem.

TL; DR

Pisząc 0.1 + 0.2w binarnej reprezentacji IEEE 754 (z dwukropkami oddzielającymi trzy części) i porównując ją z 0.3, to jest (różne bity umieściłem w nawiasach kwadratowych):

0.1 + 0.2 => 0:01111111101:0011001100110011001100110011001100110011001100110[100]
0.3       => 0:01111111101:0011001100110011001100110011001100110011001100110[011]

Po przeliczeniu z powrotem na dziesiętne wartości te to:

0.1 + 0.2 => 0.300000000000000044408920985006...
0.3       => 0.299999999999999988897769753748...

Różnica jest dokładnie 2 ^-54 , który jest ~ +5,5511151231258 × 10 ^-17 - nieznaczny (dla wielu zastosowań) w porównaniu do oryginalnych wartości.

Porównanie kilku ostatnich bitów liczby zmiennoprzecinkowej jest z natury niebezpieczne, o czym wie każdy, kto czyta słynne „ Co każdy informatyk powinien wiedzieć o arytmetyce zmiennoprzecinkowej ” (które obejmuje wszystkie główne części tej odpowiedzi).

Większość kalkulatorów używa dodatkowych cyfr ochronnych, aby obejść ten problem, co 0.1 + 0.2daje 0.3: ostatnie kilka bitów jest zaokrąglanych.

Answer 8

Liczby zmiennoprzecinkowe przechowywane w komputerze składają się z dwóch części, liczby całkowitej i wykładnika, do którego pobierana jest podstawa i mnożona przez część całkowitą.

Gdyby komputer działał w bazie 10, 0.1byłby 1 x 10⁻¹, 0.2byłby 2 x 10⁻¹i 0.3byłby 3 x 10⁻¹. Matematyka liczb całkowitych jest łatwa i dokładna, więc dodanie 0.1 + 0.2oczywiście da w wyniku 0.3.

Komputery zwykle nie działają w podstawie 10, działają w podstawie 2. Nadal można uzyskać dokładne wyniki dla niektórych wartości, na przykład 0.5jest 1 x 2⁻¹i 0.25jest 1 x 2⁻², a dodanie ich daje w wyniku 3 x 2⁻², lub 0.75. Dokładnie.

Problem polega na tym, że liczby, które można przedstawić dokładnie o podstawie 10, ale nie o podstawie 2. Liczby te należy zaokrąglić do najbliższego odpowiednika. Zakładając bardzo powszechny 64-bitowy format zmiennoprzecinkowy IEEE, najbliższa liczba to 0.1to 3602879701896397 x 2⁻⁵⁵, a najbliższa liczba to 0.2to 7205759403792794 x 2⁻⁵⁵; dodanie ich do siebie daje 10808639105689191 x 2⁻⁵⁵lub dokładną wartość dziesiętną 0.3000000000000000444089209850062616169452667236328125. Liczby zmiennoprzecinkowe są zwykle zaokrąglane do wyświetlania.

Answer 9

Błąd zaokrąglania zmiennoprzecinkowego. Z tego, co każdy informatyk powinien wiedzieć o arytmetyce zmiennoprzecinkowej :

Ściśnięcie nieskończenie wielu liczb rzeczywistych w skończoną liczbę bitów wymaga przybliżonej reprezentacji. Chociaż istnieje nieskończenie wiele liczb całkowitych, w większości programów wynik obliczeń całkowitych może być przechowywany w 32 bitach. W przeciwieństwie do tego, biorąc pod uwagę dowolną stałą liczbę bitów, większość obliczeń z liczbami rzeczywistymi da wielkości, których nie można dokładnie przedstawić za pomocą tak wielu bitów. Dlatego wynik obliczenia zmiennoprzecinkowego często musi być zaokrąglony, aby dopasować się z powrotem do jego skończonej reprezentacji. Ten błąd zaokrąglenia jest charakterystyczną cechą obliczeń zmiennoprzecinkowych.

Answer 10

Moje obejście:

function add(a, b, precision) {
    var x = Math.pow(10, precision || 2);
    return (Math.round(a * x) + Math.round(b * x)) / x;
}

precyzja odnosi się do liczby cyfr, które chcesz zachować po przecinku podczas dodawania.

Answer 11

Opublikowano wiele dobrych odpowiedzi, ale chciałbym dołączyć jeszcze jedną.

Nie wszystkie numery mogą być reprezentowane przez pływaków / podwaja Na przykład numer „0.2” zostanie przedstawiony jako „0,200000003” w pojedynczej precyzji w standardzie IEEE 754 pkt pływaka.

Model do przechowywania liczb rzeczywistych pod maską reprezentuje liczby zmiennoprzecinkowe jako

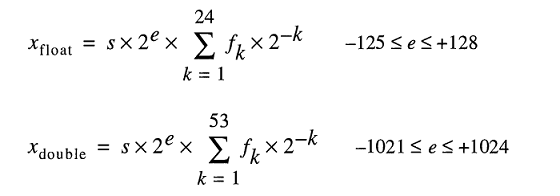
Nawet jeśli możesz pisać 0.2łatwo FLT_RADIXi DBL_RADIXwynosi 2; nie 10 dla komputera z FPU, który wykorzystuje „IEEE Standard for Binary Floating-Point Arithmetic (ISO / IEEE Std 754-1985)”.

Dlatego trochę trudno jest dokładnie przedstawić takie liczby. Nawet jeśli wyraźnie określisz tę zmienną bez żadnych pośrednich obliczeń.

Answer 12

Niektóre statystyki związane z tym słynnym pytaniem o podwójnej precyzji.

Podczas dodawania wszystkich wartości ( a + b ) z krokiem 0,1 (od 0,1 do 100) mamy ~ 15% szansy na błąd precyzji . Zwróć uwagę, że błąd może skutkować nieco większymi lub mniejszymi wartościami. Oto kilka przykładów:

0.1 + 0.2 = 0.30000000000000004 (BIGGER)
0.1 + 0.7 = 0.7999999999999999 (SMALLER)
...
1.7 + 1.9 = 3.5999999999999996 (SMALLER)
1.7 + 2.2 = 3.9000000000000004 (BIGGER)
...
3.2 + 3.6 = 6.800000000000001 (BIGGER)
3.2 + 4.4 = 7.6000000000000005 (BIGGER)

Odejmując wszystkie wartości ( a - b, gdzie a> b ) z krokiem 0,1 (od 100 do 0,1), mamy ~ 34% szansy na błąd dokładności . Oto kilka przykładów:

0.6 - 0.2 = 0.39999999999999997 (SMALLER)
0.5 - 0.4 = 0.09999999999999998 (SMALLER)
...
2.1 - 0.2 = 1.9000000000000001 (BIGGER)
2.0 - 1.9 = 0.10000000000000009 (BIGGER)
...
100 - 99.9 = 0.09999999999999432 (SMALLER)
100 - 99.8 = 0.20000000000000284 (BIGGER)

* 15% i 34% są rzeczywiście ogromne, więc zawsze używaj BigDecimal, gdy precyzja ma duże znaczenie. Przy 2 cyfrach dziesiętnych (krok 0,01) sytuacja nieco się pogarsza (18% i 36%).

Answer 13

Nie, nie jest podzielony, ale większość ułamków dziesiętnych należy podać w przybliżeniu

Podsumowanie

Arytmetyka zmiennoprzecinkowa jest dokładna, niestety nie pasuje dobrze do naszej zwykłej reprezentacji liczby dziesiętnej, więc okazuje się, że często podajemy jej dane wejściowe, które są nieco odbiegające od tego, co napisaliśmy.

Nawet proste liczby, takie jak 0,01, 0,02, 0,03, 0,04 ... 0,24, nie są reprezentowane dokładnie jako ułamki binarne. Jeśli policzysz 0,01, 0,02, 0,03 ..., dopiero gdy dojdziesz do 0,25, otrzymasz pierwszy ułamek reprezentowany w podstawie ₂ . Gdybyś spróbował tego za pomocą FP, twój 0,01 byłby nieco mniejszy, więc jedyny sposób na dodanie 25 z nich do dokładnego 0,25 wymagałby długiego łańcucha przyczynowości obejmującego bity ochronne i zaokrąglenia. Trudno to przewidzieć, więc podnosimy ręce i mówimy „FP jest niedokładne”, ale to nieprawda.

Stale dajemy sprzętowi FP coś, co wydaje się proste w podstawie 10, ale jest powtarzającym się ułamkiem w podstawie 2.

Jak to się stało?

Kiedy piszemy w systemie dziesiętnym, każdy ułamek (a konkretnie każdy kończący ułamek dziesiętny) jest wymierną liczbą postaci

           a / (2 ⁿ x 5 ^m )

W systemie binarnym otrzymujemy tylko 2 ⁿ człon, czyli:

           a / 2 ⁿ

Więc po przecinku, nie możemy reprezentować ¹ / ₃ . Ponieważ podstawa 10 zawiera 2 jako czynnik pierwszy, każda liczba, którą możemy zapisać jako ułamek binarny, może być również zapisana jako ułamek dziesiętny . Jednak trudno cokolwiek piszemy jako podstawa ₁₀ frakcji jest reprezentowalna w formacie binarnym. W zakresie od 0,01, 0,02, 0,03 ... 0,99 tylko trzy liczby mogą być reprezentowane w naszym formacie FP: 0,25, 0,50 i 0,75, ponieważ są to 1/4, 1/2 i 3/4, wszystkie liczby z czynnikiem pierwszym przy użyciu tylko 2 ⁿ wyrazu.

W podstawie ₁₀ nie może oznaczać ¹ / ₃ . Ale w binarnym, nie możemy zrobić ¹ / ₁₀ lub ¹ / ₃ .

Więc chociaż każdy ułamek binarny można zapisać w postaci dziesiętnej, sytuacja odwrotna nie jest prawdą. W rzeczywistości większość ułamków dziesiętnych powtarza się w systemie dwójkowym.

Radzenie sobie z tym

Deweloperzy są zwykle instruowani, aby wykonywać porównania <epsilon. Lepszą radą może być zaokrąglenie do wartości całkowitych (w bibliotece C: round () i roundf (), tj. Pozostanie w formacie FP), a następnie porównanie. Zaokrąglanie do określonej długości ułamka dziesiętnego rozwiązuje większość problemów z danymi wyjściowymi.

Ponadto, w przypadku problemów z obliczaniem liczb rzeczywistych (problemów, dla których wymyślono FP we wczesnych, przerażająco drogich komputerach), stałe fizyczne Wszechświata i wszystkie inne pomiary są znane tylko dla stosunkowo niewielkiej liczby znaczących cyfr, więc cała przestrzeń problemowa i tak było „niedokładne”. „Dokładność” FP nie stanowi problemu w tego rodzaju aplikacjach.

Cały problem pojawia się, gdy ludzie próbują używać FP do liczenia ziaren. To działa, ale tylko wtedy, gdy trzymasz się wartości całkowitych, co w pewnym sensie podważa sens jej używania. Dlatego mamy wszystkie te biblioteki oprogramowania ułamków dziesiętnych.

Uwielbiam odpowiedź Chrisa na temat Pizza , ponieważ opisuje rzeczywisty problem, a nie tylko zwykłe machanie ręką na temat „niedokładności”. Gdyby FP było po prostu „niedokładne”, moglibyśmy to naprawić i zrobilibyśmy to dziesiątki lat temu. Powodem, dla którego nie mamy, jest to, że format FP jest kompaktowy i szybki oraz jest najlepszym sposobem na zgniatanie wielu liczb. Jest to również dziedzictwo ery kosmosu i wyścigu zbrojeń oraz wczesnych prób rozwiązania dużych problemów z bardzo powolnymi komputerami korzystającymi z małych systemów pamięci. (Czasami pojedyncze rdzenie magnetyczne do 1-bitowej pamięci masowej, ale to już inna historia ).

Wniosek

Jeśli po prostu liczysz ziarna w banku, rozwiązania programowe, które używają reprezentacji ciągów dziesiętnych w pierwszej kolejności, działają doskonale. Ale w ten sposób nie można robić chromodynamiki kwantowej ani aerodynamiki.

Answer 14

Krótko mówiąc, to dlatego, że:

Liczby zmiennoprzecinkowe nie mogą przedstawiać wszystkich miejsc po przecinku dokładnie w systemie dwójkowym

Więc tak jak 3/10, które nie istnieje dokładnie w bazie 10 (będzie to 3,33 ... powtarzające się), tak samo 1/10 nie istnieje w systemie binarnym.

Więc co? Jak sobie z tym poradzić? Czy jest jakieś obejście?

Aby zaoferować najlepsze rozwiązanie mogę powiedzieć, że odkryłem następującą metodę:

parseFloat((0.1 + 0.2).toFixed(10)) => Will return 0.3

Pozwólcie, że wyjaśnię, dlaczego to najlepsze rozwiązanie. Jak inni wspomnieli w powyższych odpowiedziach, dobrym pomysłem jest użycie gotowej do użycia funkcji JavaScript toFixed () do rozwiązania problemu. Ale najprawdopodobniej napotkasz pewne problemy.

Wyobraź sobie, masz zamiar dodać dwa numery pływaka jak 0.2i 0.7to jest tutaj: 0.2 + 0.7 = 0.8999999999999999.

Twój oczekiwany wynik 0.9oznacza, że ​​w tym przypadku potrzebujesz wyniku z dokładnością do 1 cyfry. Więc powinieneś był użyć, (0.2 + 0.7).tofixed(1)ale nie możesz po prostu podać określonego parametru do toFixed (), ponieważ zależy to na przykład od podanej liczby

0.22 + 0.7 = 0.9199999999999999

W tym przykładzie potrzebujesz dokładności 2 cyfr, więc powinna być toFixed(2), więc jaki parametr powinien być dopasowany do każdej podanej liczby zmiennoprzecinkowej?

Można wtedy powiedzieć, że w każdej sytuacji będzie to 10:

(0.2 + 0.7).toFixed(10) => Result will be "0.9000000000"

Cholera! Co zamierzasz zrobić z tymi niechcianymi zerami po 9? Nadszedł czas, aby przekonwertować go na pływający, aby uzyskać taki, jak chcesz:

parseFloat((0.2 + 0.7).toFixed(10)) => Result will be 0.9

Teraz, gdy znalazłeś rozwiązanie, lepiej zaoferować je jako funkcję podobną do tej:

function floatify(number){
           return parseFloat((number).toFixed(10));
        }
    

Spróbujmy to sam:

function floatify(number){
       return parseFloat((number).toFixed(10));
    }
 
function addUp(){
  var number1 = +$("#number1").val(); var number2 = +$("#number2").val();
  var unexpectedResult = number1 + number2;
  var expectedResult = floatify(number1 + number2);
  $("#unexpectedResult").text(unexpectedResult); $("#expectedResult").text(expectedResult);
}
addUp();

input{
  width: 50px;
}
#expectedResult{
color: green;
}
#unexpectedResult{
color: red;
}

<script src="https://ajax.googleapis.com/ajax/libs/jquery/2.1.1/jquery.min.js"></script>
<input id="number1" value="0.2" onclick="addUp()" onkeyup="addUp()"/> +
<input id="number2" value="0.7" onclick="addUp()" onkeyup="addUp()"/> =
<p>Expected Result: <span id="expectedResult"></span></p>
<p>Unexpected Result: <span id="unexpectedResult"></span></p>

Możesz to wykorzystać w ten sposób:

var x = 0.2 + 0.7;
floatify(x);  => Result: 0.9

Jak sugeruje W3SCHOOLS , istnieje również inne rozwiązanie, możesz pomnożyć i podzielić, aby rozwiązać powyższy problem:

var x = (0.2 * 10 + 0.1 * 10) / 10;       // x will be 0.3

Pamiętaj, że (0.2 + 0.1) * 10 / 10to w ogóle nie zadziała, chociaż wydaje się to samo! Wolę pierwsze rozwiązanie, ponieważ mogę je zastosować jako funkcję, która konwertuje wejściową wartość zmiennoprzecinkową na dokładną wyjściową wartość zmiennoprzecinkową.

Answer 15

Czy wypróbowałeś rozwiązanie z taśmą klejącą?

Spróbuj określić, kiedy występują błędy i napraw je za pomocą krótkich instrukcji if, nie jest to ładne, ale w przypadku niektórych problemów jest to jedyne rozwiązanie i to jest jedno z nich.

 if( (n * 0.1) < 100.0 ) { return n * 0.1 - 0.000000000000001 ;}
                    else { return n * 0.1 + 0.000000000000001 ;}    

Miałem ten sam problem w projekcie symulacji naukowej w C # i mogę powiedzieć, że jeśli zignorujesz efekt motyla, zmieni się on w wielkiego grubego smoka i ugryzie cię w **

Answer 16

Te dziwne liczby pojawiają się, ponieważ komputery używają systemu liczb binarnych (podstawa 2) do celów obliczeniowych, podczas gdy my używamy systemu dziesiętnego (podstawa 10).

Istnieje większość liczb ułamkowych, których nie można precyzyjnie przedstawić ani w systemie dwójkowym, ani dziesiętnym, ani w obu. Wynik - zaokrąglona (ale dokładna) liczba wyników.

Answer 17

Biorąc pod uwagę, że nikt o tym nie wspomniał ...

Niektóre języki wysokiego poziomu, takie jak Python i Java, są wyposażone w narzędzia pozwalające przezwyciężyć ograniczenia binarnych liczb zmiennoprzecinkowych. Na przykład:

• decimalModuł Pythona i BigDecimalklasa Javy , które wewnętrznie reprezentują liczby w notacji dziesiętnej (w przeciwieństwie do notacji binarnej). Oba mają ograniczoną precyzję, więc nadal są podatne na błędy, jednak rozwiązują większość typowych problemów z binarną arytmetyką zmiennoprzecinkową.

  Liczby dziesiętne są bardzo dobre, gdy mamy do czynienia z pieniędzmi: dziesięć centów plus dwadzieścia centów to zawsze dokładnie trzydzieści centów:

  >>> 0.1 + 0.2 == 0.3
  False
  >>> Decimal('0.1') + Decimal('0.2') == Decimal('0.3')
  True
  

  decimalModuł Pythona jest oparty na standardzie IEEE 854-1987 .

• fractionsModuł Pythona i BigFractionklasa Apache Common . Obie reprezentują liczby wymierne jako (numerator, denominator)pary i mogą dawać dokładniejsze wyniki niż dziesiętne obliczenia zmiennoprzecinkowe.

Żadne z tych rozwiązań nie jest doskonałe (zwłaszcza jeśli patrzymy na wydajność lub wymagamy bardzo dużej precyzji), ale nadal rozwiązują one wiele problemów z binarną arytmetyką zmiennoprzecinkową.

Answer 18

Wiele z wielu duplikatów tego pytania pyta o wpływ zaokrąglania zmiennoprzecinkowego na określone liczby. W praktyce łatwiej jest zorientować się, jak to działa, patrząc na dokładne wyniki obliczeń zainteresowania, niż po prostu czytając o tym. W niektórych językach można to zrobić - na przykład konwertowanie a floatlub doubleto BigDecimalw Javie.

Ponieważ jest to pytanie niezależne od języka, wymaga narzędzi niezależnych od języka, takich jak konwerter dziesiętny na zmiennoprzecinkowy .

Odnosząc ją do liczb w pytaniu, traktowanych jako podwójne:

0,1 konwertuje na 0,1000000000000000055511151231257827021181583404541015625,

0,2 konwertuje na 0.200000000000000011102230246251565404236316680908203125,

0,3 konwertuje na 0,299999999999999988897769753748434595763683319091796875 i

0,30000000000000004 konwertuje na 0,3000000000000000444089209850062616169452667236328125.

Dodanie pierwszych dwóch liczb ręcznie lub w kalkulatorze dziesiętnym, takim jak Kalkulator pełnej precyzji , pokazuje dokładną sumę rzeczywistych danych wejściowych wynoszącą 0,3000000000000000166533453693773481063544750213623046875.

Gdyby została zaokrąglona w dół do odpowiednika 0,3, błąd zaokrąglenia wyniósłby 0,0000000000000000277555756156289135105907917022705078125. Zaokrąglenie w górę do odpowiednika 0,30000000000000004 również daje błąd zaokrąglenia 0,0000000000000000277555756156289135105907917022705078125. Rozstrzyganie remisów od rundy do równej ma zastosowanie.

Wracając do konwertera zmiennoprzecinkowego, surowa liczba szesnastkowa dla 0,30000000000000004 to 3fd3333333333334, która kończy się cyfrą parzystą i dlatego jest poprawnym wynikiem.

Answer 19

Czy mogę po prostu dodać; ludzie zawsze zakładają, że jest to problem z komputerem, ale jeśli policzysz rękami (podstawa 10), nie możesz uzyskać, (1/3+1/3=2/3)=truechyba że masz nieskończoność, aby dodać 0,333 ... do 0,333 ... tak samo jak z (1/10+2/10)!==3/10problemem w bazie 2, skracasz ją do 0,333 + 0,333 = 0,666 i prawdopodobnie zaokrągla do 0,667, co również byłoby technicznie niedokładne.

Liczenie w trójskładniku, a tercje nie stanowią problemu - może jakiś wyścig z 15 palcami na każdej dłoni zapytałby, dlaczego twoja matematyka dziesiętna została zepsuta ...

Answer 20

Ten rodzaj matematyki zmiennoprzecinkowej, który można zaimplementować w komputerze cyfrowym, z konieczności wykorzystuje przybliżenie liczb rzeczywistych i operacji na nich. (Wersja standardowa obejmuje ponad pięćdziesiąt stron dokumentacji i ma komitet zajmujący się jej erratą i dalszym udoskonalaniem.)

Przybliżenie to jest mieszaniną różnych przybliżeń, z których każde można albo zignorować, albo dokładnie wyjaśnić ze względu na specyficzny sposób odchylenia od dokładności. Obejmuje to również szereg wyraźnych wyjątkowych przypadków, zarówno na poziomie sprzętu, jak i oprogramowania, które większość ludzi przechodzi tuż obok, udając, że nie zauważają.

Jeśli potrzebujesz nieskończonej precyzji (na przykład używając liczby π zamiast jednego z wielu krótszych odstępów), powinieneś zamiast tego napisać lub użyć symbolicznego programu matematycznego.

Ale jeśli zgadzasz się z pomysłem, że czasami matematyka zmiennoprzecinkowa jest rozmyta pod względem wartości i logiki, a błędy mogą szybko się kumulować, i możesz napisać swoje wymagania i testy, aby to umożliwić, wtedy twój kod może często radzić sobie z tym, co jest w Twój FPU.

Answer 21

Dla zabawy bawiłem się reprezentacją pływaków, kierując się definicjami ze standardowego C99 i napisałem poniższy kod.

Kod wypisuje binarną reprezentację liczb zmiennoprzecinkowych w 3 oddzielnych grupach

SIGN EXPONENT FRACTION

a następnie wypisuje sumę, która po zsumowaniu z wystarczającą precyzją pokaże wartość, która naprawdę istnieje w sprzęcie.

Więc kiedy piszesz float x = 999..., kompilator przekształci tę liczbę w reprezentację bitową wydrukowaną przez funkcję w xxtaki sposób, że suma wydrukowana przez funkcję yybędzie równa podanej liczbie.

W rzeczywistości ta suma jest tylko przybliżeniem. Dla liczby 999 999 999 kompilator wstawi do bitowej reprezentacji liczby zmiennoprzecinkowej liczbę 1 000 000 000

Po kodzie dołączam sesję konsoli, w której obliczam sumę warunków dla obu stałych (bez PI i 999999999), które naprawdę istnieją w sprzęcie, wstawione tam przez kompilator.

#include <stdio.h>
#include <limits.h>

void
xx(float *x)
{
    unsigned char i = sizeof(*x)*CHAR_BIT-1;
    do {
        switch (i) {
        case 31:
             printf("sign:");
             break;
        case 30:
             printf("exponent:");
             break;
        case 23:
             printf("fraction:");
             break;

        }
        char b=(*(unsigned long long*)x&((unsigned long long)1<<i))!=0;
        printf("%d ", b);
    } while (i--);
    printf("\n");
}

void
yy(float a)
{
    int sign=!(*(unsigned long long*)&a&((unsigned long long)1<<31));
    int fraction = ((1<<23)-1)&(*(int*)&a);
    int exponent = (255&((*(int*)&a)>>23))-127;

    printf(sign?"positive" " ( 1+":"negative" " ( 1+");
    unsigned int i = 1<<22;
    unsigned int j = 1;
    do {
        char b=(fraction&i)!=0;
        b&&(printf("1/(%d) %c", 1<<j, (fraction&(i-1))?'+':')' ), 0);
    } while (j++, i>>=1);

    printf("*2^%d", exponent);
    printf("\n");
}

void
main()
{
    float x=-3.14;
    float y=999999999;
    printf("%lu\n", sizeof(x));
    xx(&x);
    xx(&y);
    yy(x);
    yy(y);
}

---

Oto sesja konsoli, w której obliczam rzeczywistą wartość liczby zmiennoprzecinkowej istniejącej w sprzęcie. Kiedyś bcdrukowałem sumę terminów wyświetlonych przez program główny. Można wstawić tę sumę w pythonie repllub czymś podobnym.

-- .../terra1/stub
@ qemacs f.c
-- .../terra1/stub
@ gcc f.c
-- .../terra1/stub
@ ./a.out
sign:1 exponent:1 0 0 0 0 0 0 fraction:0 1 0 0 1 0 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 1
sign:0 exponent:1 0 0 1 1 1 0 fraction:0 1 1 0 1 1 1 0 0 1 1 0 1 0 1 1 0 0 1 0 1 0 0 0
negative ( 1+1/(2) +1/(16) +1/(256) +1/(512) +1/(1024) +1/(2048) +1/(8192) +1/(32768) +1/(65536) +1/(131072) +1/(4194304) +1/(8388608) )*2^1
positive ( 1+1/(2) +1/(4) +1/(16) +1/(32) +1/(64) +1/(512) +1/(1024) +1/(4096) +1/(16384) +1/(32768) +1/(262144) +1/(1048576) )*2^29
-- .../terra1/stub
@ bc
scale=15
( 1+1/(2) +1/(4) +1/(16) +1/(32) +1/(64) +1/(512) +1/(1024) +1/(4096) +1/(16384) +1/(32768) +1/(262144) +1/(1048576) )*2^29
999999999.999999446351872

Otóż ​​to. W rzeczywistości wartość 999999999 jest

999999999.999999446351872

Możesz również sprawdzić, bcczy -3,14 również jest zaburzony. Nie zapomnij ustawić scalewspółczynnika bc.

Wyświetlana suma to zawartość sprzętu. Wartość uzyskana przez obliczenie jej zależy od ustawionej skali. Ustawiłem scalewspółczynnik na 15. Matematycznie, z nieskończoną precyzją, wydaje się, że jest to 1 000 000 000.

Answer 22

Inny sposób spojrzenia na to: używane są 64 bity do reprezentowania liczb. W konsekwencji nie ma możliwości dokładnego przedstawienia więcej niż 2 ** 64 = 18 446 744 073 709 551 616 różnych liczb.

Jednak Math mówi, że istnieje już nieskończenie wiele miejsc dziesiętnych między 0 a 1. IEE 754 definiuje kodowanie, aby efektywnie używać tych 64 bitów dla znacznie większej przestrzeni liczbowej plus NaN i +/- Nieskończoność, więc istnieją luki między dokładnie przedstawionymi liczbami wypełnionymi liczby tylko w przybliżeniu.

Niestety 0.3 znajduje się w luce.

Answer 23

Od Pythona 3.5 możesz używać math.isclose()funkcji do testowania przybliżonej równości:

>>> import math
>>> math.isclose(0.1 + 0.2, 0.3)
True
>>> 0.1 + 0.2 == 0.3
False

Answer 24

Wyobraź sobie, że pracujesz w systemie dziesiętnym z, powiedzmy, 8 cyframi dokładności. Sprawdzasz, czy

1/3 + 2 / 3 == 1

i dowiedz się, że to powraca false. Dlaczego? Cóż, jako liczby rzeczywiste, które mamy

1/3 = 0,333 .... i 2/3 = 0,666 ....

Obcinając do ośmiu miejsc po przecinku, otrzymujemy

0.33333333 + 0.66666666 = 0.99999999

co oczywiście różni się od 1.00000000dokładnie 0.00000001.

---

Sytuacja dla liczb binarnych ze stałą liczbą bitów jest dokładnie analogiczna. Mamy jako liczby rzeczywiste

1/10 = 0,0001100110011001100 ... (podstawa 2)

i

1/5 = 0,0011001100110011001 ... (podstawa 2)

Gdybyśmy skrócili je do, powiedzmy, siedmiu bitów, otrzymalibyśmy

0.0001100 + 0.0011001 = 0.0100101

podczas gdy z drugiej strony

3/10 = 0,01001100110011 ... (podstawa 2)

która, skrócona do siedmiu bitów, to 0.0100110, a te różnią się dokładnie 0.0000001.

---

Dokładna sytuacja jest nieco bardziej subtelna, ponieważ liczby te są zwykle przechowywane w notacji naukowej. Na przykład zamiast przechowywać 1/10, ponieważ 0.0001100możemy zapisać to jako coś podobnego 1.10011 * 2^-4, w zależności od tego, ile bitów przydzieliliśmy wykładnikowi i mantysie. Ma to wpływ na to, ile cyfr dokładności uzyskasz w swoich obliczeniach.

W rezultacie z powodu tych błędów zaokrąglania zasadniczo nigdy nie chcesz używać == na liczbach zmiennoprzecinkowych. Zamiast tego możesz sprawdzić, czy bezwzględna wartość ich różnicy jest mniejsza niż pewna ustalona mała liczba.

Answer 25

Liczby dziesiętne, takie jak 0.1, 0.2i 0.3nie są dokładnie reprezentowane w kodowanych binarnie typach zmiennoprzecinkowych. Suma przybliżeń dla 0.1i 0.2różni się od przybliżenia użytego do 0.3, stąd fałsz 0.1 + 0.2 == 0.3as można zobaczyć wyraźniej tutaj:

#include <stdio.h>

int main() {
    printf("0.1 + 0.2 == 0.3 is %s\n", 0.1 + 0.2 == 0.3 ? "true" : "false");
    printf("0.1 is %.23f\n", 0.1);
    printf("0.2 is %.23f\n", 0.2);
    printf("0.1 + 0.2 is %.23f\n", 0.1 + 0.2);
    printf("0.3 is %.23f\n", 0.3);
    printf("0.3 - (0.1 + 0.2) is %g\n", 0.3 - (0.1 + 0.2));
    return 0;
}

Wynik:

0.1 + 0.2 == 0.3 is false
0.1 is 0.10000000000000000555112
0.2 is 0.20000000000000001110223
0.1 + 0.2 is 0.30000000000000004440892
0.3 is 0.29999999999999998889777
0.3 - (0.1 + 0.2) is -5.55112e-17

Aby obliczenia te były bardziej wiarygodne, należałoby użyć reprezentacji dziesiętnej dla wartości zmiennoprzecinkowych. Standard C nie określa tych typów domyślnie, ale jako rozszerzenie opisane w raporcie technicznym .

Te _Decimal32, _Decimal64i _Decimal128typy mogą być dostępne w systemie (na przykład GCC obsługuje je na wybrane cele , ale Clang nie obsługuje ich na OS X ).

Answer 26

Ponieważ ten wątek rozgałęził się trochę na ogólną dyskusję na temat obecnych implementacji zmiennoprzecinkowych, dodam, że istnieją projekty dotyczące naprawiania ich problemów.

Spojrzeć na https://posithub.org/na przykład, który prezentuje typ liczbowy zwany posit (i jego poprzednik unum), który obiecuje lepszą dokładność przy mniejszej liczbie bitów. Jeśli moje rozumienie jest poprawne, rozwiązuje to również rodzaj problemów w pytaniu. Całkiem ciekawy projekt, za nim stoi matematyk dr John Gustafson . Całość jest open source, z wieloma rzeczywistymi implementacjami w C / C ++, Pythonie, Julii i C # (https://hastlayer.com/arithmetics).

Answer 27

To całkiem proste. Gdy masz system o podstawie 10 (taki jak nasz), może on wyrazić tylko ułamki, które używają czynnika pierwszego podstawy. Czynniki pierwsze 10 to 2 i 5. Zatem 1/2, 1/4, 1/5, 1/8 i 1/10 można wyrazić czysto, ponieważ wszystkie mianowniki używają czynników pierwszych 10. W przeciwieństwie do 1 / 3, 1/6 i 1/7 to powtarzające się ułamki dziesiętne, ponieważ ich mianowniki używają współczynnika pierwszego 3 lub 7. W systemie dwójkowym (lub o podstawie 2) jedynym czynnikiem pierwszym jest 2. Więc możesz wyrazić tylko ułamki czysto, które zawierają tylko 2 jako czynnik główny. W systemie dwójkowym 1/2, 1/4, 1/8 zostaną wyrażone czysto jako ułamki dziesiętne. Podczas gdy 1/5 lub 1/10 byłoby powtórzeniem liczb dziesiętnych. Tak więc 0,1 i 0,2 (1/10 i 1/5), podczas gdy czyste ułamki dziesiętne w systemie o podstawie 10, są powtórzeniami ułamków dziesiętnych w systemie o podstawie 2, w którym działa komputer. Kiedy wykonujesz obliczenia matematyczne na tych powtarzających się liczbach dziesiętnych, otrzymujesz resztki które są przenoszone, gdy konwertujesz podstawową liczbę 2 komputera (binarną) na bardziej czytelną dla człowieka liczbę podstawową 10.

Od https://0.30000000000000004.com/

Answer 28

Normalna arytmetyka to podstawa 10, więc ułamki dziesiętne reprezentują części dziesiąte, setne itd. Kiedy próbujesz przedstawić liczbę zmiennoprzecinkową w arytmetyce binarnej o podstawie 2, masz do czynienia z połówkami, czwartymi, ósmymi itd.

W sprzęcie zmiennoprzecinkowe są przechowywane jako mantysy całkowite i wykładniki. Mantysa reprezentuje znaczące cyfry. Wykładnik jest jak notacja naukowa, ale używa podstawy 2 zamiast 10. Na przykład 64,0 byłoby reprezentowane przez mantysę 1 i wykładnik 6. 0,125 byłoby reprezentowane przez mantysę 1 i wykładnik -3.

Liczby zmiennoprzecinkowe dziesiętne muszą sumować ujemne potęgi 2

0.1b = 0.5d
0.01b = 0.25d
0.001b = 0.125d
0.0001b = 0.0625d
0.00001b = 0.03125d

i tak dalej.

Często używa się delty błędu zamiast operatorów równości, gdy mamy do czynienia z arytmetyką zmiennoprzecinkową. Zamiast

if(a==b) ...

użyłbyś

delta = 0.0001; // or some arbitrarily small amount
if(a - b > -delta && a - b < delta) ...

Answer 29

Liczby zmiennoprzecinkowe są reprezentowane na poziomie sprzętowym jako ułamki liczb binarnych (podstawa 2). Na przykład ułamek dziesiętny:

0.125

ma wartość 1/10 + 2/100 + 5/1000 i podobnie ułamek binarny:

0.001

ma wartość 0/2 + 0/4 + 1/8. Te dwa ułamki mają tę samą wartość, jedyną różnicą jest to, że pierwszy to ułamek dziesiętny, drugi to ułamek binarny.

Niestety, większość ułamków dziesiętnych nie może mieć dokładnej reprezentacji w ułamkach dwójkowych. Dlatego generalnie liczby zmiennoprzecinkowe, które podajesz, są przybliżane tylko do ułamków binarnych, które mają być przechowywane w maszynie.

Problem jest łatwiejszy do rozwiązania przy podstawie 10. Weźmy na przykład ułamek 1/3. Możesz to przybliżyć do ułamka dziesiętnego:

0.3

albo lepiej,

0.33

albo lepiej,

0.333

itd. Bez względu na to, ile miejsc po przecinku napiszesz, wynik nigdy nie będzie równy dokładnie 1/3, ale jest to oszacowanie, które zawsze jest bliższe.

Podobnie, niezależnie od liczby miejsc dziesiętnych o podstawie 2, wartość dziesiętna 0,1 nie może być reprezentowana dokładnie jako ułamek binarny. W podstawie 2 1/10 to następująca liczba okresowa:

0.0001100110011001100110011001100110011001100110011 ...

Zatrzymaj się na dowolnej skończonej liczbie bitów, a otrzymasz przybliżenie.

W przypadku Pythona, na typowej maszynie, 53 bity są używane dla precyzji liczby zmiennoprzecinkowej, więc wartość przechowywana podczas wprowadzania dziesiętnego 0,1 jest ułamkiem binarnym.

0.00011001100110011001100110011001100110011001100110011010

która jest bliska, ale nie równa dokładnie 1/10.

Łatwo zapomnieć, że przechowywana wartość jest przybliżeniem pierwotnego ułamka dziesiętnego, ze względu na sposób wyświetlania liczb zmiennoprzecinkowych w interpretatorze. Python wyświetla tylko dziesiętne przybliżenie wartości przechowywanej w postaci binarnej. Gdyby Python miał wypisać prawdziwą wartość dziesiętną binarnego przybliżenia przechowywanego dla 0.1, to wypisze:

>>> 0.1
0.1000000000000000055511151231257827021181583404541015625

Jest to o wiele więcej miejsc po przecinku, niż by się spodziewała większość ludzi, więc Python wyświetla zaokrągloną wartość, aby poprawić czytelność:

>>> 0.1
0.1

Ważne jest, aby zrozumieć, że w rzeczywistości jest to złudzenie: przechowywana wartość nie jest dokładnie 1/10, po prostu na wyświetlaczu jest zaokrąglana przechowywana wartość. Staje się to oczywiste, gdy tylko wykonasz operacje arytmetyczne na tych wartościach:

>>> 0.1 + 0.2
0.30000000000000004

To zachowanie jest nieodłączne od samej natury reprezentacji zmiennoprzecinkowej maszyny: nie jest to błąd w Pythonie ani błąd w kodzie. Możesz zaobserwować ten sam typ zachowania we wszystkich innych językach, które używają wsparcia sprzętowego do obliczania liczb zmiennoprzecinkowych (chociaż niektóre języki domyślnie nie pokazują różnicy lub nie we wszystkich trybach wyświetlania).

W tym tkwi kolejna niespodzianka. Na przykład, jeśli spróbujesz zaokrąglić wartość 2,675 do dwóch miejsc po przecinku, otrzymasz

>>> round (2.675, 2)
2.67

Dokumentacja dotycząca prymitywu round () wskazuje, że zaokrągla on do najbliższej wartości oddalonej od zera. Ponieważ ułamek dziesiętny jest dokładnie w połowie między 2,67 a 2,68, należy spodziewać się (binarne przybliżenie) 2,68. Jednak tak nie jest, ponieważ gdy ułamek dziesiętny 2,675 jest konwertowany na liczbę zmiennoprzecinkową, jest on przechowywany w przybliżeniu, którego dokładna wartość to:

2.67499999999999982236431605997495353221893310546875

Ponieważ przybliżenie jest nieco bliższe 2,67 niż 2,68, zaokrąglenie jest w dół.

Jeśli jesteś w sytuacji, w której zaokrąglanie liczb dziesiętnych do połowy ma znaczenie, powinieneś użyć modułu dziesiętnego. Nawiasem mówiąc, moduł dziesiętny zapewnia również wygodny sposób „zobaczenia” dokładnej wartości przechowywanej dla dowolnej liczby zmiennoprzecinkowej.

>>> from decimal import Decimal
>>> Decimal (2.675)
>>> Decimal ('2.67499999999999982236431605997495353221893310546875')

Inną konsekwencją tego, że 0,1 nie jest dokładnie zapisana w 1/10, jest to, że suma dziesięciu wartości 0,1 również nie daje 1,0:

>>> sum = 0.0
>>> for i in range (10):
... sum + = 0.1
...>>> sum
0.9999999999999999

Arytmetyka binarnych liczb zmiennoprzecinkowych kryje w sobie wiele takich niespodzianek. Problem z „0.1” został szczegółowo wyjaśniony poniżej, w sekcji „Błędy reprezentacji”. Pełniejszą listę takich niespodzianek można znaleźć w artykule The Perils of Floating Point.

Prawdą jest, że nie ma prostej odpowiedzi, jednak nie bądź przesadnie podejrzliwy wobec pływających liczb virtula! Błędy w Pythonie w operacjach na liczbach zmiennoprzecinkowych wynikają z używanego sprzętu i na większości maszyn nie więcej niż 1 na 2 ** 53 na operację. Jest to więcej niż konieczne w przypadku większości zadań, ale należy pamiętać, że nie są to operacje dziesiętne, a każda operacja na liczbach zmiennoprzecinkowych może mieć nowy błąd.

Chociaż istnieją przypadki patologiczne, w większości przypadków użycia oczekiwany wynik uzyskasz na końcu, po prostu zaokrąglając w górę do liczby miejsc dziesiętnych, które chcesz na wyświetlaczu. Aby uzyskać dokładną kontrolę nad wyświetlaniem wartości zmiennoprzecinkowych, zobacz Składnia formatowania ciągów, aby zapoznać się ze specyfikacjami formatowania metody str.format ().

Ta część odpowiedzi szczegółowo wyjaśnia przykład „0,1” i pokazuje, jak samodzielnie przeprowadzić dokładną analizę tego typu przypadku. Zakładamy, że znasz binarną reprezentację liczb zmiennoprzecinkowych. Termin Błąd reprezentacji oznacza, że ​​większości ułamków dziesiętnych nie można przedstawić dokładnie binarnie. Jest to główny powód, dla którego Python (lub Perl, C, C ++, Java, Fortran i wiele innych) zwykle nie wyświetla dokładnego wyniku w postaci dziesiętnej:

>>> 0.1 + 0.2
0.30000000000000004

Dlaczego ? 1/10 i 2/10 nie można dokładnie przedstawić w ułamkach binarnych. Jednak wszystkie maszyny obecnie (lipiec 2010) są zgodne ze standardem IEEE-754 dotyczącym arytmetyki liczb zmiennoprzecinkowych. a większość platform używa „podwójnej precyzji IEEE-754” do reprezentowania elementów zmiennoprzecinkowych Pythona. IEEE-754 o podwójnej precyzji wykorzystuje 53 bity precyzji, więc podczas odczytu komputer próbuje zamienić 0,1 na najbliższy ułamek postaci J / 2 ** N, przy czym J jest liczbą całkowitą równą dokładnie 53 bitom. Przepisz:

1/10 ~ = J / (2 ** N)

w :

J ~ = 2 ** N / 10

pamiętając, że J ma dokładnie 53 bity (więc> = 2 ** 52 ale <2 ** 53), najlepsza możliwa wartość N to 56:

>>> 2 ** 52
4503599627370496
>>> 2 ** 53
9007199254740992
>>> 2 ** 56/10
7205759403792793

Tak więc 56 jest jedyną możliwą wartością dla N, która pozostawia dokładnie 53 bity dla J.Najlepszą możliwą wartością dla J jest zatem ten iloraz, zaokrąglony:

>>> q, r = divmod (2 ** 56, 10)
>>> r
6

Ponieważ przeniesienie jest większe niż połowa z 10, najlepsze przybliżenie uzyskuje się, zaokrąglając w górę:

>>> q + 1
7205759403792794

Dlatego najlepszym możliwym przybliżeniem dla 1/10 w „podwójnej precyzji IEEE-754” jest to powyżej 2 ** 56, czyli:

7205759403792794/72057594037927936

Zauważ, że ponieważ zaokrąglenie zostało wykonane w górę, wynik jest faktycznie nieco większy niż 1/10; gdybyśmy nie zaokrąglili w górę, iloraz byłby nieco mniejszy niż 1/10. Ale w żadnym wypadku nie jest to dokładnie 1/10!

Tak więc komputer nigdy nie „widzi” 1/10: widzi dokładnie ułamek podany powyżej, najlepsze przybliżenie przy użyciu liczb zmiennoprzecinkowych podwójnej precyzji z „IEEE-754”:

>>>. 1 * 2 ** 56
7205759403792794.0

Jeśli pomnożymy ten ułamek przez 10 ** 30, możemy zaobserwować wartości jego 30 miejsc po przecinku o dużej masie.

>>> 7205759403792794 * 10 ** 30 // 2 ** 56
100000000000000005551115123125L

co oznacza, że ​​dokładna wartość przechowywana w komputerze jest w przybliżeniu równa wartości dziesiętnej 0,100000000000000005551115123125. W wersjach wcześniejszych niż Python 2.7 i Python 3.1, Python zaokrąglał te wartości do 17 znaczących miejsc po przecinku, wyświetlając „0,10000000000000001”. W obecnych wersjach Pythona wyświetlana wartość to wartość, której ułamek jest możliwie najkrótszy, a po konwersji z powrotem do postaci binarnej daje dokładnie taką samą reprezentację, po prostu wyświetla „0,1”.

Answer 30

Właśnie zobaczyłem ten interesujący problem dotyczący punktów zmiennoprzecinkowych:

Rozważ następujące wyniki:

error = (2**53+1) - int(float(2**53+1))

>>> (2**53+1) - int(float(2**53+1))
1

Widzimy wyraźnie punkt przerwania, kiedy 2**53+1- wszystko działa dobrze do 2**53.

>>> (2**53) - int(float(2**53))
0

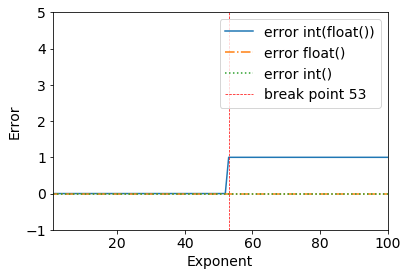
Dzieje się tak z powodu binarnego podwójnej precyzji: IEEE 754 binarny format zmiennoprzecinkowy podwójnej precyzji: binary64

Ze strony Wikipedii dla formatu zmiennoprzecinkowego podwójnej precyzji :

Binarny zmiennoprzecinkowy podwójnej precyzji jest powszechnie używanym formatem na komputerach PC, ze względu na jego szerszy zakres niż pojedyncza precyzja zmiennoprzecinkowa, pomimo wydajności i kosztu przepustowości. Podobnie jak w przypadku formatu zmiennoprzecinkowego o pojedynczej precyzji, brakuje mu precyzji liczb całkowitych w porównaniu z formatem liczb całkowitych o tym samym rozmiarze. Jest powszechnie znany po prostu jako podwójny. Standard IEEE 754 określa binary64 jako posiadający:

• Bit znaku: 1 bit
• Wykładnik: 11 bitów
• Znaczna precyzja: 53 bity (52 jawnie zapisane)

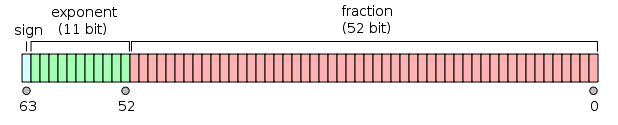
Rzeczywista wartość przyjęta przez dane 64-bitowe dane o podwójnej precyzji z podanym obciążonym wykładnikiem i 52-bitowym ułamkiem to

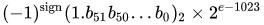
lub

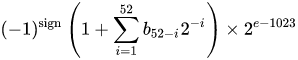
Dziękuję @a_guest za wskazanie mi tego.