Jak duży musiałby być kod QR na moim dachu, aby satelita mógł go zeskanować przy dzisiejszej dopuszczalnej rozdzielczości?

Jan 26 2021

Powiedz, używając satelitów Planet Labs

Dziękuję Ci

Odpowiedzi

7 uhoh Jan 28 2021 at 04:55

Jak duży musiałby być kod QR na moim dachu, aby satelita mógł go zeskanować przy dzisiejszej dopuszczalnej rozdzielczości?

Powiedz, używając satelitów Planet Labs

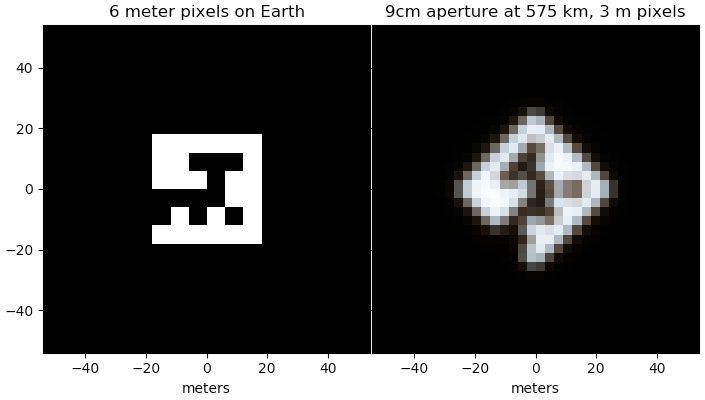
To jest dodatkowa odpowiedź. Symulowałem 6-metrowe piksele „QR” widziane z kosmosu z aperturą 9 cm (poza końcem kostki Dove 3U) przy długościach fal 450, 550 i 650 nm, obrócone o 45 stopni, a następnie próbkowane z 3-metrowymi pikselami.

To kiepski i delikatny skrypt, ale spełnia swoje zadanie.

Obraz potwierdza główny wniosek z drugiej odpowiedzi, że jest to prawdopodobnie minimalny rozmiar dla pewnej pewności widzenia go z gołębicą.

Skrypt jest nieoptymalny, byłem leniwy i korzystałem z PIL do obracania, mogłem interpolować scipy.ndimage.map_coordinates, a mogłem "fuzzified" z scipy.ndimage.gaussian_filterzamiast fantazyjnego dysku Airy.

Odcienie na ostatecznym obrazie wynikają z zależnych od długości fali granic dyfrakcji apertury, wynoszących w przybliżeniu $1.22 \lambda / D$ zmiana rozdzielczości kątowej ze stosunkiem długości fali do apertury.

import numpy as np
import matplotlib.pyplot as plt
import itertools
from PIL import Image
from scipy import special as spe
from scipy.ndimage import convolve

N = 5*2

data = ('111111' + '110001' + '111011' +
        '000011' + '010101' + '111111')
data = np.array([int(x) for x in data]).reshape((6, 6))
data = np.pad(data, ((6, 6), (6, 6)))

img = np.zeros((N*18, N*18, 3))

for i, j in itertools.product(np.arange(18), repeat=2):
    img[N*i:N*(i+1), N*j:N*(j+1)] = data[i, j]

pixsize = 6 # meters
scale = pixsize/N
extent = 9*N * scale * np.array([-1, 1, -1, 1])

R = 575 * 1000. # meters distance
x = 4*N * scale * np.linspace(-1, 1, 8*N)
X, Y = np.meshgrid(x, x)
q = np.sqrt(X**2 + Y**2)
wavelengths = 1E-09 * np.array([650, 550, 450])

a = 0.045 # radius of aperture in meters (looking out end of a 3U cubesat)
x = (2 * np.pi * a / wavelengths) * (q[..., None] / R)

# https://en.wikipedia.org/wiki/Airy_disk
airy = (2 * spe.j1(x) / x)**2
areas = airy.sum(axis=0).sum(axis=0)
airy /= areas

new = [convolve(img[..., i], airy[..., i]) for i in range(3)]
newarray = np.stack(new, axis=2)
newarray = np.uint8(255 * newarray/newarray.max())

newimg = Image.fromarray(newarray)
newimg45 = newimg.rotate(45)
newimg45.show()
n45 = np.array(list(newimg45.getdata())).reshape(18*2, N>>1, 18*2, N>>1, 3)
n45 = np.uint8(n45.sum(axis=(1, 3)) / (N>>1)**2)

if True:
    plt.figure()
    plt.subplot(1, 2, 1)
    plt.imshow(img, extent=extent)
    plt.title('6 meter pixels on Earth')
    plt.xlabel('meters')
    plt.subplot(1, 2, 2)
    plt.imshow(n45, extent=extent)
    plt.title('9cm aperture at 575 km, 3 m pixels')
    plt.xlabel('meters')
    plt.show()

4 uhoh Jan 27 2021 at 08:30

Jak duży musiałby być kod QR na moim dachu, aby satelita mógł go zeskanować przy dzisiejszej dopuszczalnej rozdzielczości?

Powiedz, używając satelitów Planet Labs

tl; dr: używając „ tagu rozszerzonej rzeczywistości ” 6x6 omówionego w odpowiedzi @ CamilleGoudeseune, takiego jak ten z łazika Curiosity i 6-metrowych pikseli (dwukrotność minimalnej rozdzielczości umożliwiającej dowolne tłumaczenie i obrót), twój wzór powinien mieć 36 x 36 metrów, aby mieć dobra zmiana w byciu zauważonym i odzyskanym z obrazu z PlanetLabs Dove.

Usunąłbym odbijanie czerwieni i podczerwieni z jasnych obszarów i kodowałbym tylko w krótszych długościach fal, ponieważ gołębie mają cztery kanały kolorów, które są (prawdopodobnie) ograniczone dyfrakcyjnie, a dłuższe długości fal mogą wtedy mieć gorszą rozdzielczość.

Spróbuj pobudzić tylko krótsze pasma fal w docelowym statku kosmicznym, aby „wyskoczyły” dla zwykłych widzów lub spójrz tylko na te długości fal w końcowym produkcie danych, jeśli szukasz siebie.

W https://www.planet.com/products/planet-imagery/Najliczniejsze satelity lub „Gołębie” dostarczają danych do produktu danych PLANETSCOPE. Mówi się, że satelity mają rozdzielczość 3,7 metra, a produkt danych ma rozmiar piksela ponownie próbkowanego 3 metry. Zobacz także @ odpowiedź DJR jest do są te obrazy z Planet Labs? Czy obrazy są publicznie dostępne?

Gdybyś miał niewiarygodne szczęście, że piksele były ustawione w jednej linii ze wzorem QR zarówno translacyjnie, jak i obrotowo, teoretycznie mogłyby mieć 3 metry.

Praktycznie jednak, biorąc pod uwagę dowolne przesunięcie i obrót wzoru w polu obrazu, powinieneś mieć współczynnik co najmniej 2, jeśli nie 3, większy niż ten.

@Uwe przypomina nam, że mały kod QR nadal byłby dość duży. Istnieje 11 x 11 mikro kodów QR, a spacefolks wykorzystały jeszcze mniejsze liczby pikseli jako alternatywy dla kodów QR z jeszcze mniejszą liczbą pikseli.