Efekt Wilsona: Jak „głębokie” są plamy słoneczne?
Niedawno dowiedziałem się o efekcie Wilsona atmosfery słonecznej. W 2009 Saas Fee zaawansowany kurs 39 stanowi:
W pobliżu kończyny słonecznej umbra [okrągły ciemny obszar plamy słonecznej] i półcień pośrodku (jaśniejsza granica plamy słonecznej) znikają. Widzimy$400-800{\rm km}$ głębiej w plamy słoneczne niż w fotosferze.
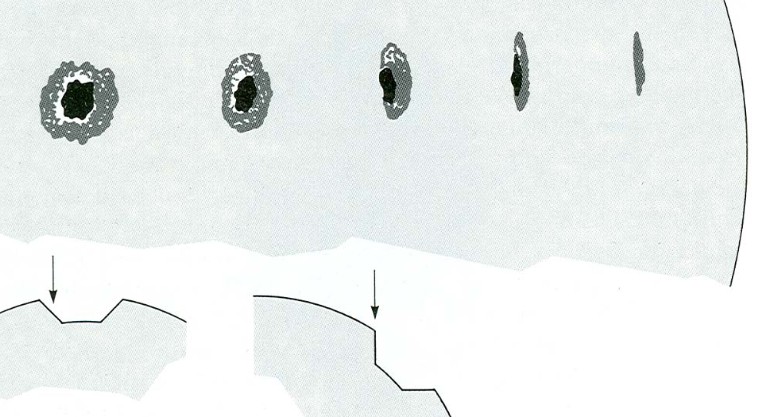
Jest też publikacja zatytułowana Plama słoneczna — płytka czy głęboka? Sołowjowa i Kirichka z 2014 roku, który w streszczeniu mówi:
Porównano dwa modele plam słonecznych – płytkie i głębokie. Według pierwszego, plama słoneczna, jako obszar zajmowany przez silne regularne pole i stosunkowo zimną plazmę, wnika w strefę konwekcji słonecznej na płytką głębokość około 4 mm. [...]
Ponadto istnieje praca doktorska Benjamina Beecka z 2015 roku, na której widać np. następujący wykres:
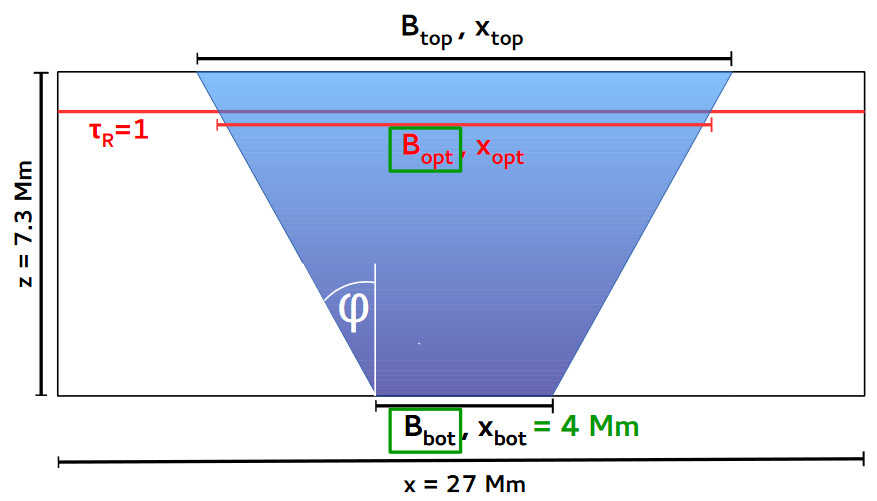
Innymi słowy, mam wartości pomiędzy $400 \ldots 7300 {\rm km}=7.3 {\rm Mm}$za głębię plamy słonecznej, która trochę mnie dezorientuje - byłbym wdzięczny, gdyby ktoś mógł mi wyjaśnić dość duży zakres głębokości. Z jednej strony interesuje mnie głębokość półcienia mierzona od półcienia (o ile można ją uznać za płaską), a z drugiej chciałabym poznać odległość od półcienia do końca ( widoczne) fotosfery, wszystko idealnie z paskami błędów.
Odpowiedzi
Ciekawe pytania! Mam nadzieję, że rzucę na nie trochę światła słonecznego.
Jak już cytujesz w streszczeniu, rozumienie i modelowanie plam słonecznych jest kwestią otwartą , zwłaszcza pytaniem o to, jak utrzymuje się stabilność plam słonecznych.
Istnieje wiele modeli, jak wskazują twoje cytaty. Po pierwsze, pewne wyjaśnienie terminologiczne: „efekt Wilsona” jest obecnie zasadniczo modelem wyjaśniającym fizykę plam słonecznych. „Depresja Wilsona” jest obserwowalnym składnikiem plamy słonecznej: geometryczna wysokość widocznej powierzchni Słońca jest obniżona w porównaniu z resztą Słońca. W czasach Wilsona była to hipoteza, ale takie depresje zostały zmierzone, np. patrz rysunek tutaj. Zasadniczo, ponieważ idea jest taka, że plama słoneczna jest generowana przez aktywność konwekcyjną pod fotosferą (tj. konwekcyjny transport ciepła jest blokowany przez intensywne pola magnetyczne, dlatego do utrzymania stabilnej plamy słonecznej potrzebne są silne pola magnetyczne), plama słoneczna może być znacznie głębiej niż jesteśmy w stanie zaobserwować, ponieważ nie możemy zobaczyć bezpośrednio pod fotosferą (ponieważ plazma słoneczna staje się zbyt nieprzezroczysta).
Istnieją inne modele wyjaśniające depresję plam słonecznych. Na przykład najnowszy model , który jest (podobno) wolny od jakichkolwiek niepewności systematycznych z powodu braku założeń zależnych od modelu, minimalizuje rozbieżność pola magnetycznego pochodzącego z obserwacji spektropolarymetrycznych. Stosując swoje ramy do obserwacji plam słonecznych, stwierdzają:
Wyprowadzona depresja Wilsona (∼600 km) jest zgodna z wynikami typowymi dla efektu Wilsona.
Ich wyniki są zgodne z wynikami badań wykorzystujących efekt Wilsona, np. jak przytaczasz z 2009 Saas Fee Advanced Course 39.
Twoje pytania:
Byłbym wdzięczny, gdyby ktoś mógł mi wyjaśnić dość duży zakres głębokości. Z jednej strony interesuje mnie głębokość półcienia mierzona od półcienia (jeśli można ją uznać za płaską), a z drugiej strony chciałabym również poznać odległość od półcienia do końca ( widoczne) fotosfery, wszystko idealnie z paskami błędów.
Stworzenie wykresu z dokładniejszymi odpowiedziami i paskami błędów wymagałoby, aby ktoś już taki wykres stworzył, lub musiałbym go stworzyć. Sam nie mam na to czasu i nie mogę znaleźć z nim opublikowanego artykułu (może tam być). Więc postaram się wyjaśnić bardziej konceptualnie. Poza tym nie możemy zobaczyć poniżej fotosfery, więc myślę, że należałoby użyć metod pośrednich, aby uzyskać paski błędów na obserwacjach głębokości umbry, z którymi mam problem (i wątpię, czy to już zostało zrobione! EDIT: zobacz sam ostatni paragraf dotyczący heliosejsmologii).
Artykuł na wiki stwierdza: „Wielkość depresji jest trudna do określenia, ale może sięgać nawet 1000 km”. Ale nie cytuje tego twierdzenia ;)
Modele efektu Wilsona, takie jak te, które cytujesz, próbują wyjaśnić pojawienie się plamy słonecznej jako pochodzącej z konwekcyjnej otoczki wnętrza gwiazdy. Czy to rozsądne?: cytowana głębokość$\sim 7.3$Mm dla tych wzrostów plazmy co najmniej w promieniu słonecznym, który wynosi $\sim 10^9$m = 1 Gm. Fotosfera znajduje się najgłębiej we wnętrzu Słońca, jakie możemy zobaczyć optycznie i rozciąga się do około 4x10$^5$m. Można więc sobie wyobrazić, że plama słoneczna może istnieć na głębokościach poniżej fotosfery wewnątrz konwekcyjnego obszaru Słońca bez zbyt głębokiego dna plamy.
EDYCJA DODANA: W modelach Sołowjowa i Kirichka, np. 2014, „stabilność plam słonecznych [jest] funkcją ich promienia i natężenia pola magnetycznego [które] zmienia się monotonicznie z promieniem od około 700 G do granicy asymptotycznej około 4000 G. Głębokość depresji Wilsona rośnie liniowo z B. Zakres stabilnej równowagi jest ograniczony w taki sposób, że większe plamy słoneczne (promień większy niż około 12–18 mm) są niestabilne, co może wyjaśniać brak bardzo dużych plam słonecznych na Słońce, a także pojawienie się mostków świetlnych w dużych plamach słonecznych dzielących je na kilka części. Plamy słoneczne z B w zakresie 2,6-2,7 kG i promieniem cienia około 2 mm są najbardziej stabilne." Cytat zaczerpnięty z przypisu 4. tego przegląd heliosejsmologii (również w ostatnim akapicie poniżej) i patrz Rysunek 22 tego przeglądu dla schematu ich modelu.
W tezie, którą cytujesz B. Beeck, głównym artykule znalezionym tutaj , geometria cienia (ani półcienia) NIE jest znana a priori, więc domyślają się i sprawdzają za pomocą swoich szczegółowych symulacji numerycznych. Systematycznie zmieniają warunki początkowe, warunki brzegowe, siłę pola magnetycznego i głębokość plamy słonecznej, aby spróbować wytworzyć fizycznie stabilną plamę słoneczną. Znależli:
Stabilne plamy słoneczne wymagają pola magnetycznego > 4kG w warstwach podpowierzchniowych. Struktura (np. gradient T) poniżej z~2-3 Mm wydaje się mieć znaczenie dla stabilności plam słonecznych. Wskazuje to również, że plamy słoneczne nie mogą być bardzo płytkimi zjawiskami. Dochodzą więc do wniosku: Stabilne plamy słoneczne wymagają pola magnetycznego o wartości B ≥ 6 kG na głębokościach 5-6 mm.
Spekulują, że ten wymóg stabilności może wykluczyć geometrie plam słonecznych, które są płaskie (tj. nie głębokie). Próbują to określić ilościowo za pomocą geometrii klina/płyty, gdzie wyższa siła pola magnetycznego na dole plamy słonecznej prowadzi do niższej intensywności cienia i bardziej wyraźnego półcienia (patrz piąty slajd od końca), co może być wykorzystane do obserwacyjnego wykluczenia pewnych geometrie plam słonecznych.
EDYCJA DODAWANA: Tak więc zakres skal zaangażowanych tutaj jest częścią aktywnego obszaru badań. Istnieje wiele teoretycznych powodów, aby podejrzewać, że plamy na Słońcu mogą być głębokie i duże, rzędu ~Mm, ale możemy badać słońce tylko tak głęboko, więc zwykle ograniczamy się do widzenia tylko rzędu ~Mm.$10^5$m, co jest zgodne z głębią fotosfery. Powoduje to, że dokładna struktura i głębokość cienia i półcienia nie są obecnie dobrze rozumiane, chociaż zależność od różnych parametrów jest dobrze rozumiana w pewnych ramach.
Zaraz po opublikowaniu tej odpowiedzi zdałem sobie sprawę, że heliosejsmologia jest sposobem na obejście problemu sondowania głębiej niż fotosfera i wydaje się to obiecujące! Postępy w heliosejsmologii od dawna oczekiwały wglądu we wnętrze Słońca, na przykład tutaj i tutaj , co dało porównywalne szacunki dla głębokości plam słonecznych, tj.$\sim$1mm. Myślę, że jest to aktywny obszar badań i będziemy z chęcią śledzić jego rozwój. Zobacz tutaj (pół-) ostatnią recenzję.