
Il y a une citation infâme attribuée à l'entraîneur et ancien joueur de la NBA Jason Kidd : "Nous allons transformer cette équipe à 360 degrés !"
Oups. Les professeurs de maths ont dû rouler des yeux à celui-là.
Comme vous le savez peut-être déjà, un cercle est composé d'exactement 360 degrés. Si Kidd avait tenu sa promesse, son équipe se serait bien retournée. Le problème, c'est que l'équipe n'arrêtait pas de tourner jusqu'à ce qu'elle ait "bouclé la boucle" et se retrouve là où elle avait commencé.
Pas une recette pour l'amélioration. Ce que Kidd cherchait, c'était de transformer son équipe à 180 degrés et d'en faire des gagnants !
Degrés, définition
Le degré , dans ce contexte, est une unité que nous pouvons utiliser pour mesurer les angles . Sur papier, les degrés sont représentés par le symbole du degré, qui ressemble à ceci : °
Ainsi, au lieu d'écrire « 18 degrés », vous pourriez simplement écrire « 18 ° » .
L' angle droit est l'un des concepts les plus importants en trigonométrie et en géométrie . C'est l'angle qui se forme à l'intersection de deux droites perpendiculaires .
Il représente également un quart de rotation complète.
Disons que vous voulez transformer physiquement quelque chose. Rien. Vous avez choisi un point central fixe et essayez de manœuvrer cet objet autour de lui dans un mouvement circulaire. Si vous terminez le travail et faites un cercle complet, c'est une rotation complète. Mais si vous arrêtez le processus à 25 % du chemin, cela ne représente qu'un quart d'une rotation complète. Ce qui vous donne un angle droit.
Un angle droit est égal à 90 degrés (c'est-à-dire 25 % de 360). Voici une autre façon de le dire : Un angle droit est égal à π/2 radians .
Temps libre! Qu'est-ce qu'un radian ? Et comment π ( pi ) s'est-il mêlé à cela ?
Déballage des radians
OK, imaginez un cercle parfait. Il y a une ligne droite qui commence à son centre exact et se termine au périmètre incurvé du cercle (comme dans le bord extérieur).
Par définition, cette ligne est le rayon de notre cercle.
Essentiellement, un radian est une tranche de cercle. Regardez le périmètre extérieur incurvé du cercle une fois de plus. Imaginez maintenant un segment du périmètre dont la longueur est égale au rayon de votre cercle. Si vous dessiniez deux lignes droites reliant ses deux extrémités au centre exact du cercle, l'angle qu'elles produiraient serait d'un radian.
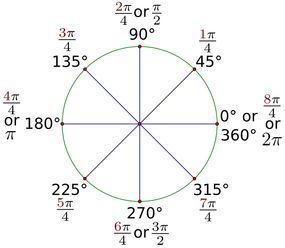
Chaque cercle a de la place pour le même nombre de radians. Ce nombre est égal à 2 fois pi ("π"). Puisque pi lui-même est égal à environ 3,14, on pourrait dire qu'il y a environ 6,28 radians dans un cercle (2 x 3,14). Ou que 1 radian est d'environ 57,29 degrés (180°/π).
Radians contre. Degrés
Écoutez, nous ne le nierons pas. Les radians peuvent être un concept plus difficile à visualiser que les degrés.
Mais ne négligez pas le premier. Ces deux unités de mesure d'angle ont leurs avantages.
Le diplôme est beaucoup plus populaire. Dans le monde réel, vous êtes plus susceptible de rencontrer des personnes qui pensent en termes de degrés plutôt qu'en radians. Donc, si vous essayez de communiquer avec un non-mathématicien, tenez-vous-en aux diplômes.
Cependant, en calcul, les radians sont excellents car ils se prêtent à des équations beaucoup plus simples . Les futurs étudiants AP voudront garder cela à l'esprit.
Conversion de degrés en radians (et vice versa)
Pour convertir des degrés en radians, il vous suffit de mémoriser quelques étapes faciles.
Tout d'abord, prenez le nombre de degrés que vous souhaitez convertir. Multipliez ce nombre par π radians/180 degrés . En éliminant certaines unités redondantes et en simplifiant un peu les choses, vous aurez votre réponse.
Supposons que vous ayez une barre de métal pliée à un angle de 120 degrés. Comment pouvons-nous exprimer cela en termes de radians?
Pour le savoir, nous écrirons notre équation comme ceci :
120 ° x (π radians/180 ° )
Remarquez la paire de symboles de degré ci-dessus. Ceux-ci s'annuleront, garantissant que notre réponse finale sera en radians. Il nous reste maintenant :
120 x (π radians/180)
Faites la multiplication et vous obtenez 120π/180 radians . Mais nous n'avons pas encore tout à fait terminé. Maintenant, nous devons simplifier notre fraction si possible. Nous devons identifier le nombre entier le plus élevé qui peut être divisé exactement à la fois en dénominateur (180) et en partie non π du numérateur (120). Spoiler alert : Dans notre cas, le nombre magique est 60.
Si vous divisez réellement 120π et 180 par 60, vous obtenez 2π/3 radians.
Alors, c'est parti : 120° est égal à 2π/3 radians.
Passer des radians aux degrés est une procédure similaire . Seulement dans ce cas, nous prendrions la quantité de départ de radians et la multiplierions par (180 ° / π ).
π/3 radians x (180 ° / π) = 60 degrés
Résumer:
Pour convertir des radians en degrés : multiplier par 180, diviser par π
Pour convertir des degrés en radians : multiplier par π, diviser par 180
Maintenant c'est intéressant
La forme "en anneau", composée de deux cercles concentriques partageant le même centre, est techniquement appelée un " anneau ".















































