Par Physique de Fermion

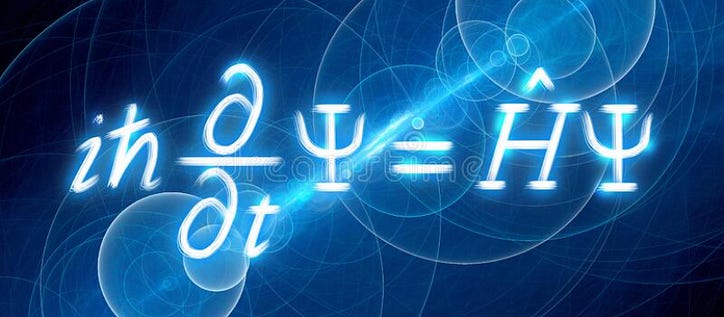
Si vous avez étudié la physique quantique, ou si vous en avez au moins entendu parler, vous avez peut-être entendu parler de ce type de Schrödinger. Vous savez - celui avec tout le truc du chat? Eh bien, il est aussi le gars derrière l'une des équations les plus utiles de la mécanique quantique - l'équation de Schrödinger. À première vue, l'équation peut sembler impossible à résoudre (et dans certains cas, elle l'est !), mais après avoir lu ceci, vous comprendrez l'équation et même comment la résoudre pour un scénario. Prêt? Allons-y.

Voici l'équation. Cela semble effrayant - il y a même des fourches dedans ! Mais essayons d'acquérir une certaine intuition sur cette équation. Nous allons d'abord commencer par parler de l'énergie en mécanique quantique, en faire la promotion auprès des opérateurs, puis parler du rôle de la fonction d'onde. Après cela, nous allons tout assembler et résoudre l'équation.

Mécanique classique

En mécanique classique (et en mécanique quantique), la formule de l'énergie est E = KE + PE où E est l'énergie totale, KE est l'énergie cinétique et PE est l'énergie potentielle. Maintenant, KE et PE prennent un peu de temps à écrire, donc pour gagner quelques millisecondes d'écriture, les physiciens utilisent les symboles évidents de T et V pour représenter respectivement l'énergie cinétique et potentielle. Alors maintenant nous avons que E = T + V

Note de bas de page : si vous avez étudié la mécanique classique, vous remarquerez peut-être que nous utilisons la formulation hamiltonienne ! Nous traiterons de la formulation lagrangienne un autre jour.

Nous savons maintenant que T=p²/2m (formule de l'énergie cinétique). Ici, m=masse, p=impulsion, et le symbole le plus dur de tous, ½=moitié. La masse est toujours constante, mais la quantité de mouvement n'a pas à l'être. Si quelqu'un applique une force à un objet, l'élan commencera à changer et s'écartera de sa valeur d'origine. Qu'en est-il de l'énergie potentielle ?

La formule de l'énergie potentielle est V= -(intégrale de F) où F est la force. Il devient évident que l'énergie potentielle dépend de la force appliquée à un objet. Dans différents scénarios, votre énergie potentielle peut prendre différentes valeurs car il existe différentes forces. Par exemple, dans un puits gravitationnel, le potentiel est V=mgx, mais dans un oscillateur harmonique, le potentiel devient V=(1/2)kx². Ceci est très important car il s'avère que nos "scénarios" où nous résolvons notre équation de Schrödinger ne sont en réalité que des potentiels différents. Cela aura un sens plus tard.

Première quantification

Maintenant, en mécanique quantique, nous prenons nos "observables" (T et E) et leur donnons un opérateurhomologues. Un opérateur pour nos besoins est juste une fonction qui prend une valeur et en recrache une autre. Ainsi, T a une contrepartie d'opérateur d'énergie cinétique, généralement désignée par un T ', et l'énergie prend une contrepartie d'opérateur d'énergie, généralement désignée par un H. L'énergie potentielle est «donnée» au lieu d'être résolue pour, donc elle n'a pas de contrepartie de l'opérateur. Maintenant, l'opérateur d'énergie cinétique est défini comme un opérateur où lorsqu'il agit sur la fonction d'onde, il renvoie l'énergie cinétique de la particule multipliée par la fonction d'onde. Même chose avec l'opérateur Énergie. Tout cela peut sembler un peu inutile et abstrait, mais croyez-moi, ce n'est pas le cas - nous y arrivons. Rappelez-vous maintenant comment T=(1/2m)p² ? Ceci implique que T' = (1/2m)p̂², où p̂ est l' opérateur moment . Et comme avant, p̂ ψ = p ψoù p est la quantité de mouvement de la particule (encore une fois, un opérateur agit sur une fonction et renvoie la fonction multipliée par la valeur liée à l'opérateur). Maintenant, il s'avère que l'opérateur momentum est

p̂ = -ih(d/dx). Prenez-le comme une donnée pour l'instant. Ceci implique que

T' = -h²/2m (d²/dx²). Et puisque E = T + V, alors H=(-h²/2m)(d²/dx²) + V. Alors nous pouvons maintenant multiplier les deux côtés par la fonction d'onde pour obtenir

H ψ = -h²/2m (d²ψ/dx²) + Vψ

Et rappelez-vous de tout à l'heure, H ψ = Eψ, donc

Eψ = (-h²/2m)(d²ψ/dx²) + Vψ

Maintenant, respirez profondément. Nous avons fait beaucoup de calculs et j'espère que vous n'êtes pas perdu. Il s'avère que nous venons de « dériver » l'équation de Schrödinger ! Maintenant, avant de parler de le résoudre, nous devons parler de ce qu'est même cette "fonction d'onde".

Qu'est-ce qu'une fonction d'onde ?

En mécanique classique, nous utilisons l'équation hamiltonienne classique pour résoudre les équations de mouvement d'une particule. Les équations du mouvement ne sont que les équations de l'endroit où se trouve une particule à un moment donné dans le temps. Par exemple, l'équation du mouvement d'une particule libre est x(t)=vt + x0. Nous pouvons trouver la position de la particule à n'importe quel moment si nous avons la position initiale et la vitesse. En mécanique quantique, nous utilisons à la place l'équation de Schrödinger pour trouver ce qu'on appelle la « fonction d'onde ». La fonction d'onde elle-même n'a pas de sens physique — elle ne veut rien dire et ne vous dit rien (directement). Ce qui est significatif, c'est le carré de la fonction d'onde qui vous donne la densité de probabilité. La densité de probabilité n'est qu'une fonction qui vous indique la probabilité que vous trouviez une particule dans une certaine plage lorsque vous la mesurez. On peut donc dire que la fonction d'onde n'est que la « racine carrée » de la densité de probabilité. Maintenant, nous avons enfin toutes les connaissances de base pour parler de ce qu'est l'équation de Schrödinger .

Comme nous pouvons le voir dans l'équation ci-dessus, tout est constant à l'exception de l'énergie potentielle V(x). Nous prenons une énergie potentielle particulière et résolvons l'équation pour le cas où vous avez cette énergie potentielle particulière. C'est tellement beau, car peu importe les contraintes qui s'exercent sur votre système, ou la chaleur, la charge, la tension, etc., vous n'avez pas besoin de tenir compte de tout cela. Tout ce que vous devez savoir, c'est juste la fonction d'énergie potentielle et vous pouvez résoudre l'équation

(Si nous voulons être pédants ici, nous pourrions dire que "techniquement", nous incorporons toutes ces choses à l'intérieur du potentiel lui-même. De plus, le triangle à l'envers est l'abréviation de la dérivée seconde)

Calcul

(si vous n'aimez pas le calcul, vous pouvez sauter cette partie)

Maintenant, résolvons l'équation de Schrödinger pour un potentiel simple où V(x)=0 partout. C'est ce qu'on appelle une particule libre, puisque les forces nettes sur elle sont nulles. C'est libre de toute oppression ! Dans le cas classique, l'équation du mouvement serait x(t)=vt + x0 qui forme une droite sur un graphe spatio-temporel. Voyons à quoi ressemble la fonction d'onde pour le cas quantique.

Puisque V(x)=0, alors l'équation de schrodinger devient

-h²/2m(d² ψ/dx²) = Eψ

Nous pouvons alors faire quelques réarrangements et obtenir

d² ψ/dx² = -2mEψ/h²

Nous pouvons maintenant voir que tous les termes du membre de droite sont constants à l'exception de ψ. C'est bien car cela rend l'équation facile à résoudre. Nous pouvons alors définir une constante k comme étant sqrt(2mE/h), ce qui signifie que nous avons maintenant

d²ψ / dx² = -k²ψ

Nous additionnons ensuite les deux côtés de l'équation par le terme de droite

d²ψ/dx² + k²ψ = 0

On suppose alors que ψ(x) = exp(rx)

et à partir de là on obtient

r=-k², r= +ik ou -ik

Cela signifie que ψ( x)=exp(ikx) ou

ψ( x)=exp(-ikx)

Puisque l'équation est linéaire, nous pouvons prendre une superposition (combinaison linéaire) des deux parties pour obtenir la solution générale

ψ(x) = Aexp(ikx) + Bexp(-ikx)

et nous avons techniquement terminé. Vous vous demandez peut-être comment nous pouvons même déterminer les constantes A et B. Nous le ferions généralement par quelque chose appelé normalisation, mais c'est une autre histoire. Il s'avère que ce scénario ne peut pas être normalisé. C'est un langage sophistiqué car la fonction d'onde ne s'approche pas de zéro lorsque vous allez à l'infini ou moins l'infini. Alors pour quelles valeurs A et B correspondent à cet état ? Eh bien, il s'avère que ce n'est pas réellement un état possible puisque vous ne pouvez pas le normaliser. Oops!

Ne vous inquiétez pas ! Il s'avère qu'une superposition de toutes les fonctions d'onde possibles peut produire un état réel. Cela apporte beaucoup de choses intéressantes en soi - mais c'est aussi une histoire pour la prochaine fois.

Merci d'avoir lu! Ce site Web fait un travail terrible pour formater les symboles mathématiques, donc une partie du texte mathématique ne s'affiche pas bien. Si vous voulez voir une dérivation vidéo de la même chose, j'ai fait une vidéo ici sur ma chaîne Fermion Physics sur la solution (même si je parle assez vite). Basculer entre la vidéo et cet article aidera à rendre la solution plus claire. Jusqu'à la prochaine fois!