Statistik - Beta-Verteilung

Die Beta-Verteilung stellt eine kontinuierliche Wahrscheinlichkeitsverteilung dar, die durch zwei positive Formparameter, $ \ alpha $ und $ \ beta $, parametrisiert wird, die als Exponenten der Zufallsvariablen x erscheinen und die Form der Verteilung steuern.

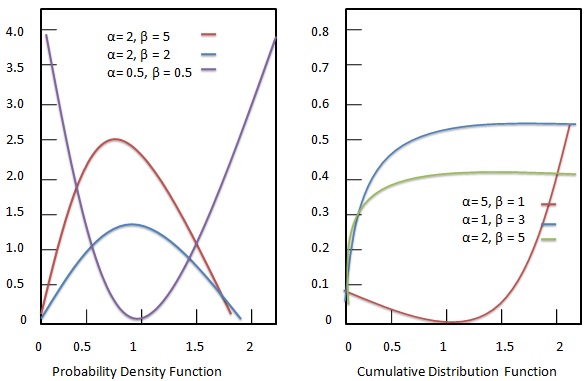
Wahrscheinlichkeitsdichtefunktion

Die Wahrscheinlichkeitsdichtefunktion der Beta-Verteilung ist gegeben als:

Formel

$ {f (x) = \ frac {(xa) ^ {\ alpha-1} (bx) ^ {\ beta-1}} {B (\ alpha, \ beta) (ba) ^ {\ alpha + \ beta- 1}} \ hspace {.3in} a \ le x \ le b; \ alpha, \ beta> 0 \\ [7pt] \, wobei \ B (\ alpha, \ beta) = \ int_ {0} ^ {1} {t ^ {\ alpha-1} (1-t) ^ { \ beta-1} dt}} $

Wo -

$ {\ alpha, \ beta} $ = Formparameter.
$ {a, b} $ = obere und untere Grenze.
$ {B (\ alpha, \ beta)} $ = Beta-Funktion.

Standard Beta Distribution

Bei oberen und unteren Grenzen von 1 und 0 wird die Beta-Verteilung als Standard-Beta-Verteilung bezeichnet. Es wird durch folgende Formel angetrieben:

Formel

$ {f (x) = \ frac {x ^ {\ alpha-1} (1-x) ^ {\ beta-1}} {B (\ alpha, \ beta)} \ hspace {.3in} \ le x \ le 1; \ alpha, \ beta> 0} $

Verteilungsfunktion

Die kumulative Verteilungsfunktion der Beta-Verteilung ist gegeben als:

Formel

$ {F (x) = I_ {x} (\ alpha, \ beta) = \ frac {\ int_ {0} ^ {x} {t ^ {\ alpha-1} (1-t) ^ {\ beta- 1} dt}} {B (\ alpha, \ beta)} \ hspace {.2in} 0 \ le x \ le 1; p, \ beta> 0} $

Wo -

$ {\ alpha, \ beta} $ = Formparameter.
$ {a, b} $ = obere und untere Grenze.
$ {B (\ alpha, \ beta)} $ = Beta-Funktion.

Es wird auch als unvollständiges Beta-Funktionsverhältnis bezeichnet.