Statistik - Zentraler Grenzwertsatz

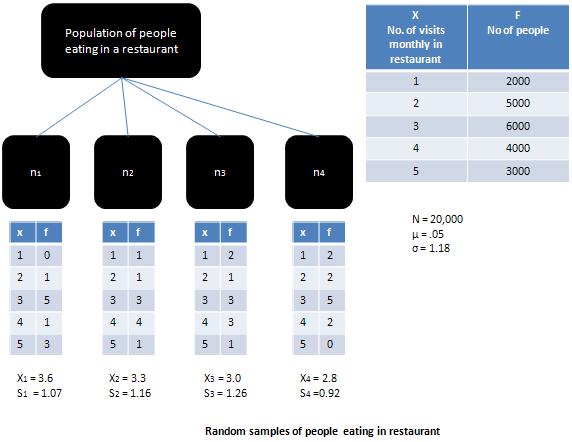
Wenn die Population, aus der die Stichprobe gezogen wurde, eine normale Population ist, dann ist die sample means wäre gleich dem Bevölkerungsdurchschnitt und dem sampling distributionwäre normal. Wenn die Population mehr verzerrt ist, wie dies in Abbildung dargestellt ist, wird diesampling distribution würde dazu neigen, sich der Normalverteilung zu nähern, vorausgesetzt, die Probe ist groß (dh größer als 30).

Gemäß Central Limit Theoremfür ausreichend große Proben mit einer Größe von mehr als 30 ist die Form der sampling distribution wird immer mehr wie ein normal distribution, unabhängig von der Form der Elternbevölkerung. Dieser Satz erklärt die Beziehung zwischen dempopulation distribution und sampling distribution. Es unterstreicht die Tatsache, dass, wenn es genügend Proben gibt, diesampling distribution von mittleren Ansätzen normal distribution. Die Bedeutung des zentralen Grenzwertsatzes wurde von Richard zusammengefasst. I. Levin in den folgenden Worten:

Die Bedeutung des zentralen Grenzwertsatzes liegt in der Tatsache, dass wir Stichprobenstatistiken verwenden können, um Rückschlüsse auf Populationsparameter zu ziehen, ohne etwas über die Form der Häufigkeitsverteilung dieser Population zu wissen, außer dem, was wir aus der Stichprobe erhalten können.