Statistik - F-Verteilung
Die F-Verteilung (Snedecors F-Verteilung oder Fisher-Snedecor-Verteilung) stellt eine kontinuierliche Wahrscheinlichkeitsverteilung dar, die häufig als Nullverteilung der Teststatistik auftritt. Dies geschieht hauptsächlich während der Varianzanalyse oder des F-Tests.
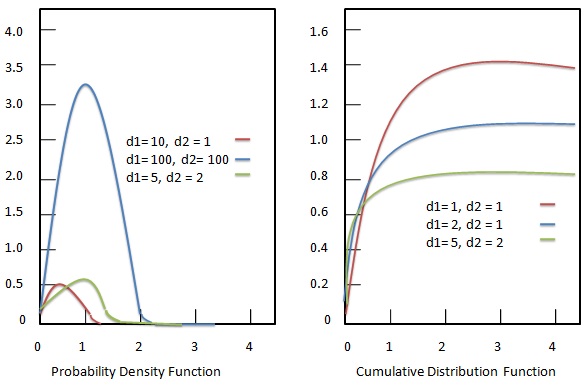
Wahrscheinlichkeitsdichtefunktion
Die Wahrscheinlichkeitsdichtefunktion der F-Verteilung ist gegeben als:
Formel
Wo -
$ {d_1} $ = positiver Parameter.
$ {d_2} $ = positiver Parameter.
$ {x} $ = Zufallsvariable.
Verteilungsfunktion
Die kumulative Verteilungsfunktion der F-Verteilung ist gegeben als:
Formel
$ {F (x; d_1, d_2) = I _ {\ frac {d_1x} {d_1x + d_2}} (\ frac {d_1} {2}, \ frac {d_2} {2})} $
Wo -
$ {d_1} $ = positiver Parameter.
$ {d_2} $ = positiver Parameter.
$ {x} $ = Zufallsvariable.
$ {I} $ = niedrigere unvollständige Beta-Funktion.