Statistik - Chi-Quadrat-Verteilung

Die Chi-Quadrat-Verteilung (Chi-Quadrat oder $ {X ^ 2} $ - Verteilung) mit Freiheitsgraden k ist die Verteilung einer Summe der Quadrate von k unabhängigen normalen Standard-Zufallsvariablen. Es ist eine der am häufigsten verwendeten Wahrscheinlichkeitsverteilungen in der Statistik. Es ist ein Sonderfall der Gammaverteilung.

Die Chi-Quadrat-Verteilung wird von Statistikern häufig verwendet, um Folgendes zu berechnen:

Schätzung des Konfidenzintervalls für eine Populationsstandardabweichung einer Normalverteilung unter Verwendung einer Stichprobenstandardabweichung.
Überprüfung der Unabhängigkeit von zwei Kriterien zur Klassifizierung mehrerer qualitativer Variablen.
Überprüfen der Beziehungen zwischen kategorialen Variablen.
Untersuchung der Stichprobenvarianz bei normaler Verteilung.
Um Abweichungen von Unterschieden zwischen erwarteten und beobachteten Frequenzen zu testen.
So führen Sie einen Chi-Quadrat-Test durch (ein Anpassungstest).

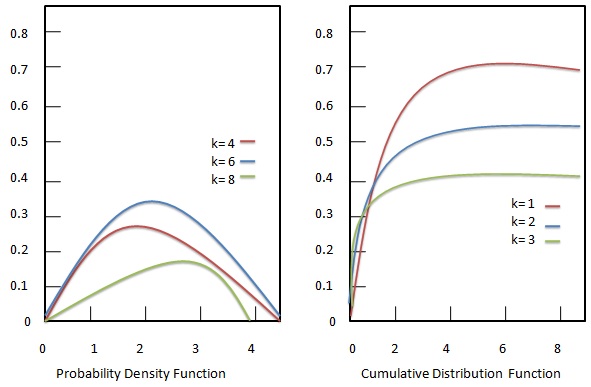
Wahrscheinlichkeitsdichtefunktion

Die Wahrscheinlichkeitsdichtefunktion der Chi-Quadrat-Verteilung ist gegeben als:

Formel

$ {f (x; k) =} $ $ \ begin {Fälle} \ frac {x ^ {\ frac {k} {2} - 1} e ^ {- \ frac {x} {2}}} {2 ^ {\ frac {k} {2}} \ Gamma (\ frac {k} {2})}, & \ text {if $ x \ gt 0 $} \\ [7pt] 0, & \ text {if $ x \ le 0 $} \ end {Fälle} $

Wo -

$ {\ Gamma (\ frac {k} {2})} $ = Gammafunktion mit geschlossenen Formularwerten für den ganzzahligen Parameter k.
$ {x} $ = Zufallsvariable.
$ {k} $ = ganzzahliger Parameter.