Statistik - Venn-Diagramm

Das Venn-Diagramm ist eine Möglichkeit, die Beziehung zwischen Gruppen von Entitäten oder Objekten visuell darzustellen. Venn-Diagramme bestehen aus Kreisen, wobei jeder Kreis eine ganze Menge darstellt. Das Venn-Diagramm kann unbegrenzt viele Kreise haben, im Allgemeinen werden jedoch zwei oder drei Kreise bevorzugt, da das Diagramm sonst zu komplex wird.

Schritte zum Zeichnen eines Venn-Diagramms

Betrachten Sie die folgenden Personengruppen:

Cricket Players - $ C = \ {Ram, Shyam, Mohan, Rohan, Ramesh, Suresh \} $
Hockey Players - $ H = \ {Ramesh, Naresh, Mahesh, Leela, Sunita \} $

Schritt 1: Zeichnen Sie ein Rechteck und beschriften Sie es als Spieler.

Schritt 2: Zeichnen Sie zwei Kreise und kennzeichnen Sie sie als Cricket und Hockey. Stellen Sie sicher, dass sich die Kreise überlappen.

Schritt 3: Schreiben Sie relevante Namen in den Kreis. Gemeinsame Namen sollten in die gemeinsame Region fallen.

Union

Union ($ \ cup $) stellt eine Menge dar, in der Elemente in allen Kategorien vorhanden sind, aber nicht wiederholt werden.

Beispiel

Problem Statement:

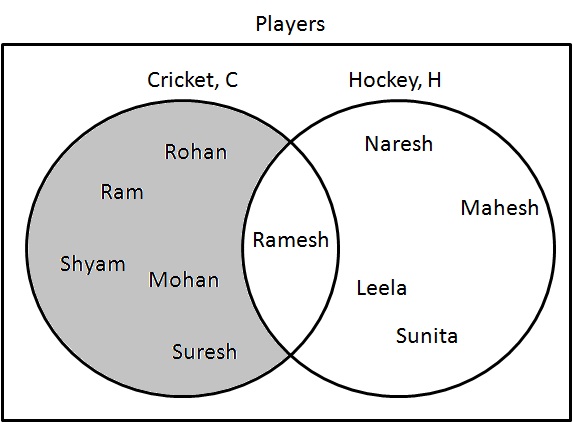
Zeichnen Sie ein Venn-Diagramm von $ C \ cup H $.

Solution:

Schritt 1: Bestimmen Sie die Spieler, die entweder Cricket oder Hockey spielen. Zeichnen Sie sie wie folgt:

$ C \ cup H = \ {Ram, Shyam, Mohan, Rohan, Ramesh, Suresh, Naresh, Mahesh, Leela, Sunita \} $.

Überschneidung

Der Schnittpunkt ($ \ cap $) stellt eine Menge dar, in der Elemente in beiden Kategorien vorhanden sind.

Beispiel

Problem Statement:

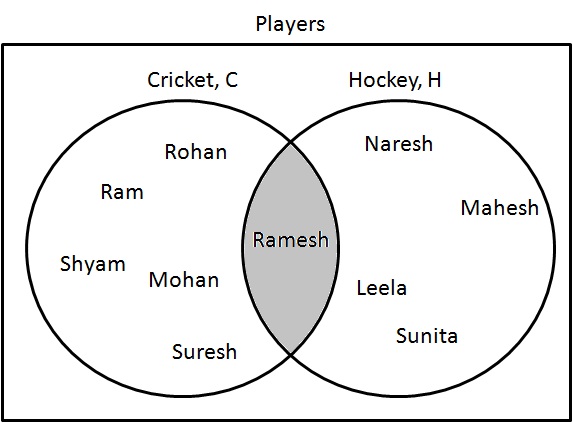
Zeichnen Sie ein Venn-Diagramm von $ C \ cap H $.

Solution:

Schritt 1: Bestimmen Sie die Spieler, die beide Cricket und Hockey spielen. Zeichnen Sie sie wie folgt:

$ C \ cap H = \ {Ramesh \} $.

Unterschied

Der Unterschied ($ - $) stellt eine Menge dar, bei der Elemente nur in einer Kategorie und nicht in einer anderen vorhanden sind.

Beispiel

Problem Statement:

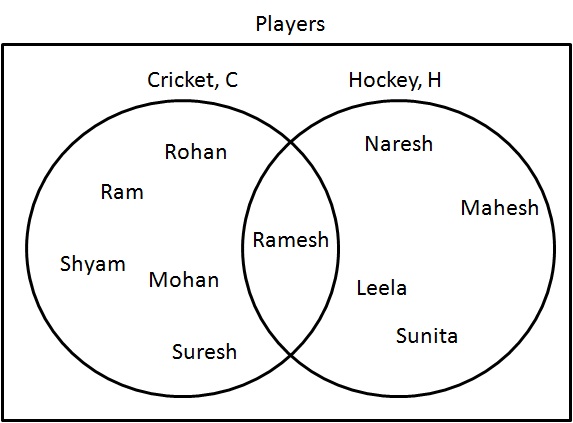
Zeichnen Sie ein Venn-Diagramm von $ C - H $.

Solution:

Schritt 1: Bestimmen Sie die Spieler, die nur Cricket spielen. Zeichnen Sie sie wie folgt:

$ C - H = \ {Ram, Shyam, Mohan, Rohan, Suresh \} $.