Statistik - Vergleiche vergleichen
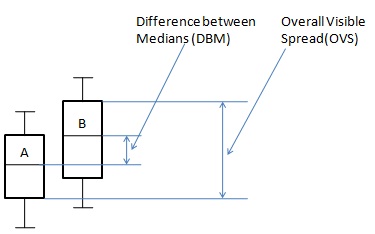
Bevölkerungsgruppen können mit Box- und Whisker-Plots verglichen werden. Die insgesamt sichtbare Streuung und der Unterschied zwischen dem Median werden verwendet, um den Schluss zu ziehen, dass zwischen zwei Gruppen tendenziell ein Unterschied besteht oder nicht.
Fall 2: Formel
$ {P = \ frac {DBM} {OVS} \ times 100} $
Wo -
$ {P} $ = prozentuale Differenz
$ {DBM} $ = Unterschied zwischen Medianen.
$ {OVS} $ = Sichtbare Gesamtverteilung.
Regeln
Bei einer Stichprobengröße von 30 besteht bei einem Prozentsatz von mehr als 33% tendenziell ein Unterschied zwischen zwei Gruppen.
Bei einer Stichprobengröße von 100 besteht bei einem Prozentsatz von mehr als 20% tendenziell ein Unterschied zwischen zwei Gruppen.
Bei einer Stichprobengröße von 1000 besteht bei einem Prozentsatz von mehr als 10% tendenziell ein Unterschied zwischen zwei Gruppen.
Beispiel
Problemstellung:
Beschreiben Sie den Unterschied zwischen den folgenden Datensätzen.
| Sr. Nr. | Name | Stellen Sie A ein | Set B. |
|---|---|---|---|
| 1 | Max | 12 | 15 |
| 2 | UQ | 10 | 13 |
| 3 | Median | 7 | 10 |
| 4 | LQ | 6 | 9 |
| 5 | Mindest | 5 | 6 |
Lösung:
Betrachten Sie das folgende Diagramm:
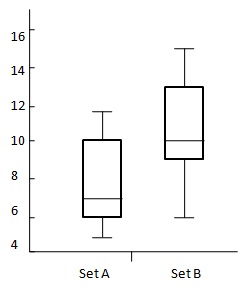
$ {OVS = 13 - 6 \\ [7pt] \ = 7 \\ [7pt] \ DBM = 10 -3 \\ [7pt] \ = 4} $
Wenden Sie die Formel an
$ {P = \ frac {DBM} {OVS} \ mal 100 \\ [7pt] \ = \ frac {4} {7} \ mal 100 \\ [7pt] \ = 57,14} $
Da der Prozentsatz über 33% liegt, gibt es einen Unterschied zwischen Satz A und Satz B. Es ist wahrscheinlich, dass Satz B größer als Satz A ist.