Statistik - Kumulative Poissonverteilung
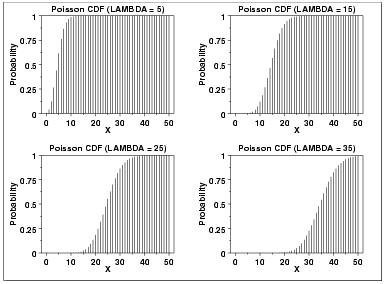
$ {\ lambda} $ ist der Formparameter, der die durchschnittliche Anzahl von Ereignissen in dem angegebenen Zeitintervall angibt. Das Folgende ist die Darstellung der Poisson-Wahrscheinlichkeitsdichtefunktion für vier Werte von $ {\ lambda} $. Verteilungsfunktion.
Formel
$$ {F (x, \ lambda) = \ sum_ {k = 0} ^ x \ frac {e ^ {- \ lambda} \ lambda ^ x} {k!}} $$
Wo -
$ {e} $ = Die Basis des natürlichen Logarithmus ist gleich 2.71828
$ {k} $ = Die Anzahl der Vorkommen eines Ereignisses; deren Wahrscheinlichkeit durch die Funktion gegeben ist.
$ {k!} $ = Die Fakultät von k
$ {\ lambda} $ = Eine positive reelle Zahl, die der erwarteten Anzahl von Vorkommen während des angegebenen Intervalls entspricht
Beispiel
Problem Statement:
Ein komplexes Softwaresystem macht durchschnittlich 7 Fehler pro 5.000 Codezeilen. Wie hoch ist die Wahrscheinlichkeit von genau 2 Fehlern in 5.000 Zeilen zufällig ausgewählter Codezeilen?
Solution:
Die Wahrscheinlichkeit von genau 2 Fehlern in 5.000 Zeilen zufällig ausgewählter Codezeilen beträgt: