Statistik - Normalverteilung
Eine Normalverteilung ist eine Anordnung eines Datensatzes, bei dem sich die meisten Werte in der Mitte des Bereichs sammeln und der Rest sich symmetrisch zu beiden Extremen hin verjüngt. Die Größe ist ein einfaches Beispiel für etwas, das einem normalen Verteilungsmuster folgt: Die meisten Menschen sind durchschnittlich groß, die Anzahl der Personen, die größer und kleiner als der Durchschnitt sind, ist ziemlich gleich, und eine sehr kleine (und immer noch ungefähr gleichwertige) Anzahl von Personen ist entweder extrem groß oder extrem kurz. Hier ist ein Beispiel für eine Normalverteilungskurve:
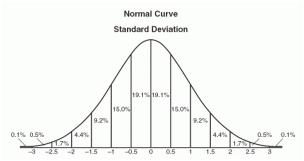
Eine grafische Darstellung einer Normalverteilung wird aufgrund ihrer aufgeweiteten Form manchmal als Glockenkurve bezeichnet. Die genaue Form kann je nach Verteilung der Population variieren, aber der Peak liegt immer in der Mitte und die Kurve ist immer symmetrisch. In einer Normalverteilung sind der Mittelwert und der Median alle gleich.
Formel
$ {y = \ frac {1} {\ sqrt {2 \ pi}} e ^ {\ frac {- (x - \ mu) ^ 2} {2 \ sigma}}} $
Wo -
$ {\ mu} $ = Mittelwert
$ {\ sigma} $ = Standardabweichung
$ {\ pi \ ca. 3.14159} $
$ {e \ ca. 2.71828} $
Beispiel
Problem Statement:
Eine Umfrage zur täglichen Reisezeit ergab folgende Ergebnisse (in Minuten):
| 26 | 33 | 65 | 28 | 34 | 55 | 25 | 44 | 50 | 36 | 26 | 37 | 43 | 62 | 35 | 38 | 45 | 32 | 28 | 34 |
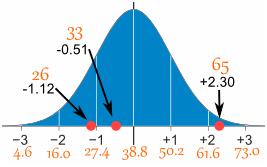
Der Mittelwert beträgt 38,8 Minuten und die Standardabweichung 11,4 Minuten. Konvertieren Sie die Werte in Z-Scores und erstellen Sie das Normalverteilungsdiagramm.
Solution:
Die Formel für den Z-Score, die wir verwendet haben:
$ {z = \ frac {x - \ mu} {\ sigma}} $
Wo -
$ {z} $ = der "Z-Score" (Standard Score)
$ {x} $ = der zu standardisierende Wert
$ {\ mu} $ = Mittelwert
$ {\ sigma} $ = die Standardabweichung
So konvertieren Sie 26:
Subtrahieren Sie zuerst den Mittelwert: 26-38,8 = -12,8,
Teilen Sie dann durch die Standardabweichung: -12,8 / 11,4 = -1,12
26 ist also -1,12 Standardabweichung vom Mittelwert
Hier sind die ersten drei Konvertierungen.
| Originalwert | Berechnung | Standard Score (Z-Score) |
|---|---|---|
| 26 | (26-38,8) / 11,4 = | -1.12 |
| 33 | (33-38,8) / 11,4 = | -0,51 |
| 65 | (65-38,8) / 11,4 = | -2,30 |
| ... | ... | ... |
Und hier stellen sie grafisch dar: