Statistik - Exponentialverteilung
Die Exponentialverteilung oder die negative Exponentialverteilung stellt eine Wahrscheinlichkeitsverteilung dar, um die Zeit zwischen Ereignissen in einem Poisson-Prozess zu beschreiben. Im Poisson-Prozess treten Ereignisse kontinuierlich und unabhängig mit einer konstanten Durchschnittsrate auf. Die Exponentialverteilung ist ein besonderer Fall der Gammaverteilung.
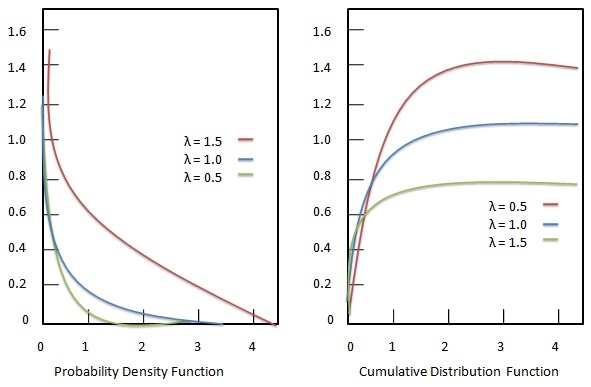
Wahrscheinlichkeitsdichtefunktion
Die Wahrscheinlichkeitsdichtefunktion der Exponentialverteilung ist gegeben als:
Formel
$ {f (x; \ lambda) =} $ $ \ begin {case} \ lambda e ^ {- \ lambda x}, & \ text {wenn $ x \ ge 0 $} \\ [7pt] 0, & \ Text {wenn $ x \ lt 0 $} \ end {Fälle} $
Wo -
$ {\ lambda} $ = Ratenparameter.
$ {x} $ = Zufallsvariable.
Verteilungsfunktion
Die kumulative Verteilungsfunktion der Exponentialverteilung ist gegeben als:
Formel
$ {F (x; \ lambda) =} $ $ \ begin {case} 1- e ^ {- \ lambda x}, & \ text {if $ x \ ge 0 $} \\ [7pt] 0, & \ Text {wenn $ x \ lt 0 $} \ end {Fälle} $
Wo -
$ {\ lambda} $ = Ratenparameter.
$ {x} $ = Zufallsvariable.