Statistik - Gammaverteilung

Die Gammaverteilung repräsentiert kontinuierliche Wahrscheinlichkeitsverteilungen der Zwei-Parameter-Familie. Gammaverteilungen werden im Allgemeinen mit drei Arten von Parameterkombinationen entwickelt.

Ein Formparameter $ k $ und ein Skalierungsparameter $ \ theta $.
Ein Formparameter $ \ alpha = k $ und ein inverser Skalierungsparameter $ \ beta = \ frac {1} {\ theta} $, der als Ratenparameter bezeichnet wird.
Ein Formparameter $ k $ und ein Mittelwertparameter $ \ mu = \ frac {k} {\ beta} $.

Jeder Parameter ist eine positive reelle Zahl. Die Gammaverteilung ist die maximale Entropiewahrscheinlichkeitsverteilung, die durch folgende Kriterien bestimmt wird.

Formel

$ {E [X] = k \ theta = \ frac {\ alpha} {\ beta} \ gt 0 \ und \ ist \ fest. \\ [7pt] E [ln (X)] = \ psi (k) + ln (\ theta) = \ psi (\ alpha) - ln (\ beta) \ und \ ist \ fest. } $

Wo -

$ {X} $ = Zufällige Variable.
$ {\ psi} $ = Digammafunktion.

Charakterisierung mit Form $ \ alpha $ und Rate $ \ beta $

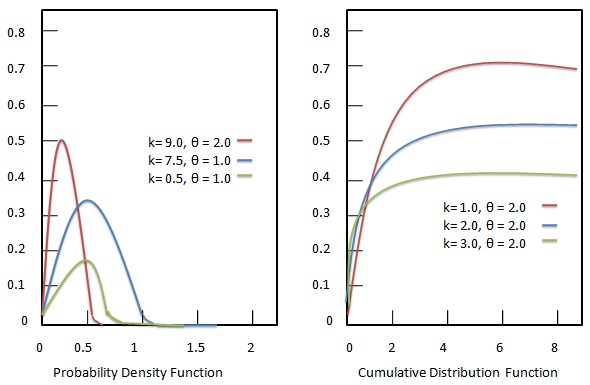
Wahrscheinlichkeitsdichtefunktion

Die Wahrscheinlichkeitsdichtefunktion der Gammaverteilung ist gegeben als:

Formel

$ {f (x; \ alpha, \ beta) = \ frac {\ beta ^ \ alpha x ^ {\ alpha - 1} e ^ {- x \ beta}} {\ Gamma (\ alpha)} \ where \ x \ ge 0 \ und \ \ alpha, \ beta \ gt 0} $

Wo -

$ {\ alpha} $ = Standortparameter.
$ {\ beta} $ = Skalierungsparameter.
$ {x} $ = Zufallsvariable.

Verteilungsfunktion

Die kumulative Verteilungsfunktion der Gammaverteilung ist gegeben als:

Formel

$ {F (x; \ alpha, \ beta) = \ int_0 ^ xf (u; \ alpha, \ beta) du = \ frac {\ gamma (\ alpha, \ beta x)} {\ Gamma (\ alpha)} } $

Wo -

$ {\ alpha} $ = Standortparameter.
$ {\ beta} $ = Skalierungsparameter.
$ {x} $ = Zufallsvariable.
$ {\ gamma (\ alpha, \ beta x)} $ = niedrigere unvollständige Gammafunktion.

Charakterisierung mit Form $ k $ und Skala $ \ theta $

Wahrscheinlichkeitsdichtefunktion

Die Wahrscheinlichkeitsdichtefunktion der Gammaverteilung ist gegeben als:

Formel

$ {f (x; k, \ theta) = \ frac {x ^ {k - 1} e ^ {- \ frac {x} {\ theta}}} {\ theta ^ k \ Gamma (k)} \ where \ x \ gt 0 \ und \ k, \ theta \ gt 0} $

Wo -

$ {k} $ = Formparameter.
$ {\ theta} $ = Skalierungsparameter.
$ {x} $ = Zufallsvariable.
$ {\ Gamma (k)} $ = Gammafunktion, die bei k ausgewertet wird.

Verteilungsfunktion

Die kumulative Verteilungsfunktion der Gammaverteilung ist gegeben als:

Formel

$ {F (x; k, \ theta) = \ int_0 ^ xf (u; k, \ theta) du = \ frac {\ gamma (k, \ frac {x} {\ theta})} {\ Gamma (k )}} $

Wo -

$ {k} $ = Formparameter.
$ {\ theta} $ = Skalierungsparameter.
$ {x} $ = Zufallsvariable.
$ {\ gamma (k, \ frac {x} {\ theta})} $ = niedrigere unvollständige Gammafunktion.