Fizyka Fermiona

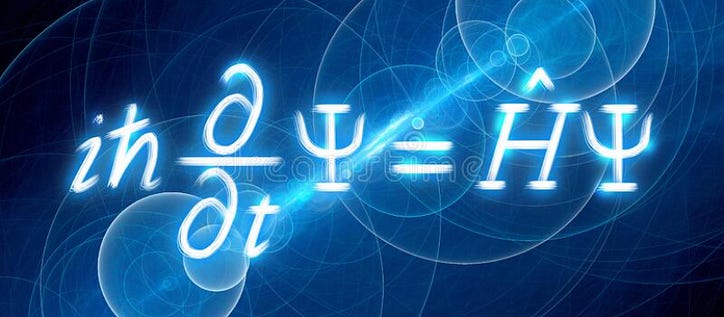
Jeśli studiowałeś fizykę kwantową lub przynajmniej o niej słyszałeś, być może słyszałeś o tym gościu ze Schrodingera. Wiesz - ten z całym kotem? Cóż, jest także twórcą jednego z najbardziej użytecznych równań w mechanice kwantowej — równania Schrodingera. Na pierwszy rzut oka równanie może wydawać się niemożliwe do rozwiązania (i rzeczywiście w niektórych przypadkach jest!), Ale po przeczytaniu tego równania zrozumiesz to równanie, a nawet zrozumiesz, jak je rozwiązać dla jednego scenariusza. Gotowe? Chodźmy.

Oto równanie. Wygląda przerażająco — ma nawet widły! Ale spróbujmy uzyskać trochę intuicji w tym równaniu. Zaczniemy od omówienia energii w mechanice kwantowej, promując ją wśród operatorów, a następnie porozmawiamy o roli funkcji falowej. Następnie zszyjemy wszystko razem i rozwiążemy równanie.

Mechanika klasyczna

W mechanice klasycznej (i mechanice kwantowej) wzór na energię to E = KE + PE, gdzie E to energia całkowita, KE to energia kinetyczna, a PE to energia potencjalna. Teraz zapisanie KE i PE zajmuje trochę czasu, więc aby zaoszczędzić kilka milisekund pisania, fizycy używają oczywistych symboli T i V, aby przedstawić odpowiednio energię kinetyczną i potencjalną. Więc teraz mamy, że E = T + V

Przypis: Jeśli znasz mechanikę klasyczną, możesz zauważyć, że używamy sformułowania Hamiltona! Sformułowaniem Lagrange'a zajmiemy się kiedy indziej.

Teraz wiemy, że T=p²/2m (wzór na energię kinetyczną). Tutaj m = masa, p = pęd i najtrudniejszy ze wszystkich symboli, ½ = połowa. Masa jest zawsze stała, ale pęd nie musi być. Jeśli ktoś przyłoży siłę do obiektu, pęd zacznie się zmieniać i odbiega od swojej pierwotnej wartości. A co z energią potencjalną?

Wzór na energię potencjalną to V= -(całka z F), gdzie F jest siłą. Staje się oczywiste, że energia potencjalna zależy od siły przyłożonej do obiektu. W różnych scenariuszach twoja energia potencjalna może przybierać różne wartości, ponieważ istnieją różne siły. Na przykład w studni grawitacyjnej potencjał wynosi V=mgx, ale w oscylatorze harmonicznym potencjał wynosi V=(1/2)kx². Jest to bardzo ważne, ponieważ okazuje się, że nasze „scenariusze”, w których rozwiązujemy równanie Schrodingera, to tak naprawdę różne potencjały. To będzie miało sens później.

Pierwsza kwantyzacja

Teraz w mechanice kwantowej bierzemy nasze „obserwowalne” (T i E) i sprawiamy, że mają operatoraodpowiedniki. Dla naszych celów operator jest po prostu funkcją, która pobiera jedną wartość i wypluwa inną. Tak więc T ma odpowiednik operatora energii kinetycznej, zwykle oznaczany przez T', a energia przyjmuje odpowiednik operatora energii, zwykle oznaczany przez H. Energia potencjalna jest „dana”, a nie rozwiązana, więc nie ma żadnego odpowiednik operatora. Teraz operator energii kinetycznej jest zdefiniowany jako operator, w którym działając na funkcję falową, zwraca energię kinetyczną cząstki pomnożoną przez funkcję falową. To samo z operatorem energetycznym. Cała ta sprawa może wydawać się nieco bezużyteczna i abstrakcyjna, ale uwierzcie mi, że tak nie jest — docieramy do celu. Pamiętasz teraz, jak T=(1/2m)p²? Oznacza to, że T' = (1/2m)p̂², gdzie p̂ jest operatorem pędu . I tak jak poprzednio, p̂ ψ = p ψgdzie p jest pędem cząstki (ponownie, operator działa na funkcję i zwraca funkcję pomnożoną przez dowolną wartość związaną z operatorem). Teraz okazuje się, że operator pędu jest

p̂ = -ih(d/dx). Na razie traktuj to jako pewnik. To daje do zrozumienia ze

T' = -h²/2m (d²/dx²). A skoro E = T + V, to H=(-h²/2m)(d²/dx²) + V. Teraz możemy pomnożyć obie strony przez funkcję falową, aby otrzymać

H ψ = -h²/2m (d²ψ/dx²) + Vψ

I pamiętajcie z wcześniejszego H ψ = Eψ, więc

mi ψ = ( -h² /2m)(d²ψ/dx²) + Vψ

Teraz weź głęboki oddech. Zrobiliśmy dużo matematyki i mam nadzieję, że się nie zgubiłeś. Okazuje się, że właśnie „wyprowadziliśmy” równanie Schrodingera! Teraz, zanim porozmawiamy o rozwiązaniu tego problemu, musimy porozmawiać o tym, czym w ogóle jest ta „funkcja falowa”.

Co to jest funkcja falowa?

W mechanice klasycznej używamy klasycznego równania Hamiltona do rozwiązywania równań ruchu cząstki. Równania ruchu to po prostu równania określające położenie cząstki w danym momencie. Na przykład równanie ruchu cząstki swobodnej to x(t)=vt + x0. Możemy znaleźć położenie cząstki w dowolnym momencie, jeśli mamy położenie początkowe i prędkość. W mechanice kwantowej zamiast tego używamy równania Schrodingera, aby znaleźć coś, co nazywa się „funkcją falową”. Sama funkcja falowa nie ma fizycznego znaczenia — nic nie znaczy i nic ci nie mówi (bezpośrednio). Znaczący jest kwadrat funkcji falowej, który daje gęstość prawdopodobieństwa. Gęstość prawdopodobieństwa to po prostu funkcja, która mówi o prawdopodobieństwie znalezienia cząstki w pewnym zakresie podczas jej pomiaru. Możemy więc powiedzieć, że funkcja falowa jest po prostu „pierwiastkiem kwadratowym” gęstości prawdopodobieństwa. Teraz w końcu mamy całą podstawową wiedzę, aby porozmawiać o tym, czym jest równanie Schrodingera .

Jak widać z powyższego równania, wszystko jest stałe z wyjątkiem energii potencjalnej V(x). Bierzemy określoną energię potencjalną i rozwiązujemy równanie dla przypadku, w którym masz tę konkretną energię potencjalną. To jest takie piękne, ponieważ nie ma znaczenia, jakie obciążenia występują w twoim systemie, ani ciepło, ładunek, napięcie, jak to nazwiesz - nie musisz uwzględniać żadnego z nich. Wszystko, co musisz wiedzieć, to tylko funkcja energii potencjalnej i możesz rozwiązać równanie

(Jeśli chcemy być tutaj pedantyczni, możemy powiedzieć, że „technicznie” włączamy wszystkie te rzeczy do samego potencjału. Również odwrócony trójkąt jest skrótem od drugiej pochodnej)

Obliczenie

(jeśli nie lubisz rachunku różniczkowego, możesz pominąć tę część)

Teraz rozwiążmy równanie Schrodingera dla prostego potencjału, w którym V(x)=0 wszędzie. Nazywa się to cząstką swobodną, ​​ponieważ działające na nią wypadkowe siły są równe zeru. Jest wolny od wszelkich ucisków! W klasycznym przypadku równanie ruchu miałoby postać x(t)=vt + x0, co tworzy linię prostą na wykresie czasoprzestrzennym. Zobaczmy, jak wygląda funkcja falowa dla przypadku kwantowego.

Skoro V(x)=0, to równanie Schrodingera ma postać

-h²/2m(d² ψ/dx²) = Eψ

Możemy wtedy dokonać pewnych zmian i uzyskać

d² ψ/dx² = -2mEψ/h²

Widzimy teraz, że wszystkie wyrazy po prawej stronie są stałe z wyjątkiem ψ. Jest to dobre, ponieważ ułatwia rozwiązanie równania. Możemy wtedy zdefiniować stałą k jako sqrt(2mE/h), co oznacza, że ​​teraz mamy

d²ψ / dx² = -k²ψ

Następnie dodajemy obie strony równania przez prawą rękę

d²ψ/dx² + k²ψ = 0

Zakładamy wtedy, że ψ(x) = exp(rx)

i z tego mamy

r=-k², r= +ik lub -ik

Oznacza to, że ψ( x)=exp(ikx) lub

ψ( x)=exp(-ikx)

Ponieważ równanie jest liniowe, możemy przyjąć superpozycję (kombinację liniową) obu części, aby uzyskać ogólne rozwiązanie

ψ(x) = Aexp(ikx) + Bexp(-ikx)

i technicznie jesteśmy skończeni. Być może zastanawiasz się, jak możemy w ogóle wyznaczyć stałe A i B. Zwykle robimy to za pomocą czegoś, co nazywamy normalizacją, ale to historia na inną okazję. Okazuje się, że dla tego scenariusza nie da się znormalizować. To wymyślny język dla funkcji falowej, która nie zbliża się do zera w miarę zbliżania się do nieskończoności lub minus nieskończoności. Więc dla jakich wartości A i B odpowiadają temu stanowi? Cóż, okazuje się, że w rzeczywistości nie jest to możliwy stan, ponieważ nie można go znormalizować. Ups!

Nie martw się! Okazuje się, że superpozycja wszystkich możliwych funkcji falowych może dać stan rzeczywisty. To przynosi wiele fajnych rzeczy – ale to też jest historia na następny raz.

Dziękuje za przeczytanie! Ta witryna kiepsko radzi sobie z formatowaniem symboli matematycznych, więc część tekstu matematycznego nie była dobrze wyświetlana. Jeśli chcesz zobaczyć wyprowadzenie wideo tej samej rzeczy, zrobiłem film tutaj na moim kanale Fermion Physics na temat rozwiązania (chociaż mówię dość szybko). Przełączanie między filmem a tym artykułem pomoże wyjaśnić rozwiązanie. Do następnego razu!