
Frakcje. Rachunek różniczkowy. Liczby urojone . Jeśli masz lęk przed matematyką , jak wielu z nas, słowa takie jak te wywołują niepokojące wspomnienia lekcji matematyki w liceum, kiedy bazgroły na tablicy były zarówno mylące, jak i otępiająco nudne. - Dlaczego w ogóle kogoś obchodzi matematyka? poskarżyliśmy się. "Jaki jest sens?"
Michael Brooks to rozumie. Brytyjski dziennikarz może mieć doktorat. Jest doktorem fizyki kwantowej i pracuje jako redaktor w New Scientist , ale rozumie, dlaczego tak wielu z nas nie znosi „matematyki” (jak mówią w Wielkiej Brytanii). W szkole matematyka może być strasznie nudna, a kiedy staje się bardziej interesująca, matematyka staje się niemal mistyczną, niepoznawalną siłą zrozumiałą tylko dla Stephena Hawkinga .
Ale w swojej fascynującej i przystępnej nowej książce „ The Art of More: How Mathematics Created Civilization ” Brooks przedstawia przekonujący argument, że niektóre z największych osiągnięć ludzkości były możliwe tylko dzięki matematyce. Matematyka nie tylko nie jest nudna, ale też nie jest tajemnicza. To praktyczny sposób rozwiązywania problemów, który uczynił nasz świat lepszym miejscem od starożytnej Sumerii po Dolinę Krzemową.
Oto cztery kolorowe historie, które ilustrują, jak prosta (i nie taka prosta) matematyka zmieniła nasz świat.
1. All Hail Shulgi, król dodawania
Około 4000 lat temu starożytne miasto Ur było jedną z wielkich stolic Sumeru w południowej Mezopotamii. Rewolucja agrarna umożliwiła osiedlom o bezprecedensowej wielkości, ale kapłanom i królom coraz trudniej było śledzić zbiory zboża, magazynowanie i wypłaty, aby nakarmić zarówno bogów, jak i ludzi.
Potrzebowali oczywiście matematyki. Na początku nic nadzwyczajnego, tylko podstawowa arytmetyka (dodawanie, odejmowanie, mnożenie, dzielenie). A jednym z pierwszych mistrzów arytmetyki, według starożytnych glinianych tabliczek znalezionych w Ur, był facet o imieniu King Shulgi.
„Istnieją nagrania hymnów, które śpiewano o jego zdolności do dodawania rzeczy” – mówi Brooks. „Sprawił, że jego poddani czcili go za jego zdolności matematyczne”.
Shulgi nie tylko popisywał się swoimi boskimi umiejętnościami matematycznymi; zbudował coś, co uczeni uznają za „pierwszy stan matematyczny”, mówi Brooks. Matematyka była wykorzystywana głównie w księgowości, co pozwoliło Shulgiemu i jego skrybom zachować ścisłą kontrolę nad finansami Ur i zapobiec oszukiwaniu państwa.
Można by argumentować, że Shulgi i jego skrybowie byli niczym innym, jak tylko uwielbionymi audytorami, ale audytowanie, jak pisze Brooks w „Sztuce więcej”, jest „prawdziwą kolebką cywilizacji”.

„Shulgi zdał sobie sprawę, że kiedy już przejmiesz kontrolę nad liczbami, zaczyna to być bardzo dochodowe finansowo” – mówi Brooks. „Ta rzecz z matematyką działa”.
Wykorzystując matematykę do pracy, Shulgi i Ur wzbogacili się ogromnie i wykorzystali to bogactwo do rozwoju jednej z najwcześniejszych i największych cywilizacji na świecie. Shulgi przypisuje się zbudowaniu Wielkiego Zigguratu w Ur, zbudowaniu rozległej sieci dróg i poszerzeniu swojego imperium handlowego o społeczności arabskie i indusu.
2. Rewolucja francuska rozpoczęła się od księgowego

XVIII-wieczny francuski monarcha Ludwik XVI pomógł sfinansować amerykańską rewolucję , ale Francja pogrążyła się w długach. Król potrzebował dobrego księgowego, aby pomóc zbilansować księgi, więc mianował swojego ministra finansów genewskiego bankiera o nazwisku Jacques Necker .
Ale Necker był trochę „zbyt dobry” w swojej pracy. Upublicznił budżet — nietypowy dla monarchii absolutnej — i używał podwójnej księgowości, aby dokładnie śledzić wydatki. Brooks mówi, że Necker wierzył, że zrównoważone księgi to nie tylko dobra księgowość, ale także podstawa moralnego, zamożnego, szczęśliwego i potężnego rządu.
„Rozrzutny francuski dwór królewski nie lubił tego, ponieważ oznaczało to, że nie mogli wydawać pieniędzy na wszystko, co chcieli”, mówi Brooks. – Więc Necker został zwolniony.
Przyjaciele króla mogli pogardzać Neckerem, ale rewolucjoniści go kochali. W rzeczywistości to zwolnienie Neckera było iskrą, która zapaliła beczkę prochu rewolucji francuskiej .
„Nieśli na ramionach popiersie Jacquesa Neckera, gdy szturmowali Bastylię” – mówi Brooks. „To fajny księgowy”.
3. Kepler wynalazł rachunek całkowy, aby zaoszczędzić pieniądze na winie
Niemiecki astronom Johannes Kepler słynie ze swoich praw ruchu planet , które dowiodły, że planety w naszym Układzie Słonecznym krążą wokół Słońca po eliptycznych torach, ale napisał też całą książkę o prawidłowym kształcie beczek po winie.
Podobno Kepler zamówił beczkę wina na swój drugi ślub w austriackim mieście Linz, ale kiedy nadszedł czas, aby zapłacić za wino, wybuchła kłótnia. Keplerowi nie podobała się metoda, którą handlarz winem używał do wyceny beczki.
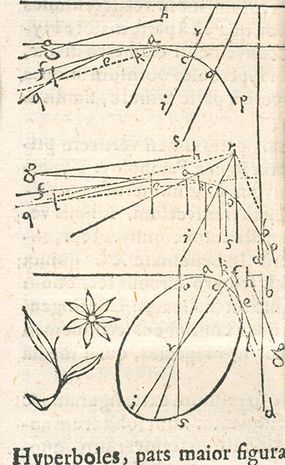
Zgodnie ze zwyczajem handlarz winem położył beczkę na boku i wbił długi pręt przez otwór w środku beczki, aż uderzył w przeciwległy róg. Pręt został usunięty, a koszt wina został określony na podstawie tego, ile pręta było mokre.
Kepler szybko zorientował się, gdzie ta metoda się nie sprawdziła: cena za tę samą ilość wina zmieniałaby się wraz z wymiarami beczki. Długa i cienka beczka kosztowałaby mniej niż krótka i gruba. Kepler zrzędliwie zapłacił rachunek, ale nie mógł porzucić pytania, jak skonstruować beczkę, która daje najwięcej wina za twoje pieniądze.
Metoda Keplera polegała na obliczeniu objętości zakrzywionej beczki na wino, wyobrażając ją sobie jako stos płaskich cylindrów. Aby jednak uzyskać najdokładniejszy wynik, musisz użyć wielu cylindrów. W rzeczywistości muszą być nieskończenie małe, aby wypełnić każdy cal przestrzeni wewnątrz beczki. „A kiedy dzielimy czas, odległość lub cokolwiek innego na nieskończenie małe”, pisze Brooks w swojej książce, „jesteśmy w królestwie rachunku różniczkowego”.
W 1615 Kepler opublikował „Nova Stereometria Dolorium Vinariorum” lub „ Nową geometrię beczek z winem ”, uważaną obecnie za podstawowy tekst rachunku całkowego .
Pokazując, jak zmaksymalizować wymiary beczki na wino, aby zminimalizować jej cenę (nawiasem mówiąc, beczki austriackie były na miejscu), Kepler wskazał drogę do wykorzystania rachunku różniczkowego do maksymalizacji wydajności wszelkiego rodzaju rzeczy. Brooks wykorzystuje współczesne przykłady obliczania właściwej dawki leku przeciwnowotworowego, aby zapewnić najskuteczniejszą odpowiedź, lub ile paliwa powinien zabrać 747, aby podróżować najdalej bez obciążania.
4. Liczby urojone zelektryfikowały Amerykę dosłownie
Nic tak nie pobudza do matematyki jak liczby urojone. Matematyka jest wystarczająco trudna, gdy używamy rzeczywistych liczb! Teraz chcesz, żebyśmy pobawili się wyimaginowanymi liczbami?
Uspokój się, mówi Brooks. Okazuje się, że liczby urojone są bardzo realne; po prostu mają naprawdę głupie imię.
Problem zaczął się, gdy matematycy próbowali rozwiązać równania kwadratowe, które wymagały pierwiastka kwadratowego z liczby ujemnej. Ponieważ niemożliwe jest, aby jakakolwiek liczba razy sama w sobie równała się ujemna (nawet ujemna razy ujemna równa się dodatnia), matematycy zaczęli nazywać takie liczby „liczbami urojonymi”.
Liczby urojone mogłyby pozostać dziwną matematyczną osobliwością, gdyby nie urodzony na 4 stopy, 9-calowy (1,45-metrowy) fenomen Karl August Rudolf Steinmetz, ale lepiej znany jako Charles Proteus Steinmetz.

Steinmetz odkrył, jak wykorzystać liczby urojone do rozwiązania jednego z najtrudniejszych problemów inżynieryjnych lat 90. XIX wieku: jak wykorzystać ekscytującą nową moc elektryczności i dostarczyć ją do domów i firm. Podczas gdy ważniacy, tacy jak Thomas Edison i Nikola Tesla , spierali się o korzyści płynące z prądu przemiennego w porównaniu z prądem stałym, inżynierowie zmagali się z niewiarygodnie złożoną matematyką wymaganą do zbudowania funkcjonujących obwodów elektrycznych.
„Charles Steinmetz wymyślił wzór na zrobienie tych wszystkich naprawdę trudnych obliczeń i przekształcenie ich w naprawdę łatwe, wykorzystujące liczby urojone” – mówi Brooks. „W zasadzie tak zelektryfikowaliśmy Amerykę”.
Formuły Steinmetza napędzały erę elektryczności i dokonywały wielkich postępów w uprzemysłowieniu i odkryciach naukowych. Pół wieku później Bill Hewlett i David Packard wykorzystali wyimaginowane liczby do zaprojektowania swojego pierwszego produktu, oscylatora audio, w swoim garażu w Palo Alto w Kalifornii, znanym jako „miejsce narodzin Doliny Krzemowej”.
zarabia niewielką prowizję partnerską, gdy dokonujesz zakupów za pośrednictwem linków na naszej stronie.
Teraz to jest fajne
Urodzony z garbusem Steinmetz był mały, ale potężny. Słynnie zdiagnozował wadliwy generator w fabryce samochodów Henry'ego Forda , słuchając, jak pracuje przez dwa dni, a następnie rysując kredą znak na gigantycznej maszynie, w której inżynierowie musieli wymienić 16 cewek drutu. Brooks mówi, że kiedy Ford sprzeciwił się fakturze na 10 000 dolarów i poprosił o wyjaśnienie, Steinmetz odpowiedział szczegółowym rachunkiem: „Zrobienie znaku kredą na generatorze: 1 USD. Wiedząc, gdzie zrobić znak: 9 999 USD”.















































