Có thể sử dụng cây Stern-Brocot để hội tụ tốt hơn $2^m/3^n$?
Đọc tiên quyết:
- Bất kỳ thực dương nào có thể được gần đúng như $2^m/3^n$ với $(m,n)$ đủ lớn?
- Chuỗi cây Brocot nghiêm ngặt
Lý do tại sao tôi đã tìm kiếm một quy trình không có nhược điểm này, tức là trong đó giá trị gần đúng tiếp theo luôn gần hơn với kết quả mong muốn. Đây là những gì tôi đã cố gắng cho đến nay.
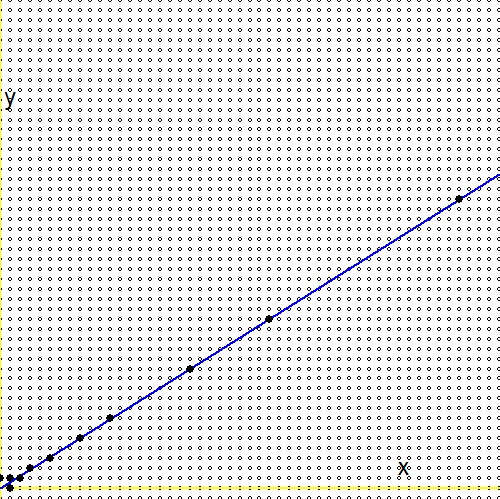
Theo câu hỏi (2.), với mọi số thực dương$0 \lt g \lt 1$, tồn tại một dãy vô hạn trong cây Stern Brocot [..] hội tụ đến số thực. Trong khi đó, câu hỏi này có câu trả lời và kết quả chính trong đó như sau: $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$ Theo quan điểm của câu hỏi (1.), chúng tôi thay thế $\ln(2)/\ln(3)$ cho số đó $g$. Sau đó, nó sau đó: $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$Có thể hình dung cuộc tìm kiếm qua cây Stern-Brocot. Đường màu xanh lam là hàm $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$, vòng tròn nhỏ là phân số, được ánh xạ trên lưới $\,m/n \to (m,n)\,$, các chấm màu đen có khối lượng lớn là các phân số trong cây Stern-Brocot. Người ta thấy rằng tìm kiếm qua cây hiệu quả hơn nhiều so với việc tăng $m$ và $n$ với các gia số tại một thời điểm.
Bây giờ so sánh biểu thức ở dòng thứ hai của các công thức trên với một biểu thức tương tự trong tham chiếu (1.): $$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$ Và hãy chuẩn bị cho một sự thất vọng: logarit của số thực tùy ý $r$bị mất tích! Hay cách khác:$\ln(r)=0$ hoặc là $r=1$. Điều này có nghĩa là "tìm kiếm vô hạn" của chúng tôi thông qua cây Stern-Brocot, mặc dù có hiệu quả cao, cuối cùng chỉ đạt được giá trị gần đúng cho số một. Tôi thấy điều này thật kỳ lạ, bởi vì - về mặt đồ họa - dường như không có sự khác biệt lớn giữa$\color{red}{2^m/3^n \to r}$ và $\color{blue}{2^m/3^n \to 1}$:
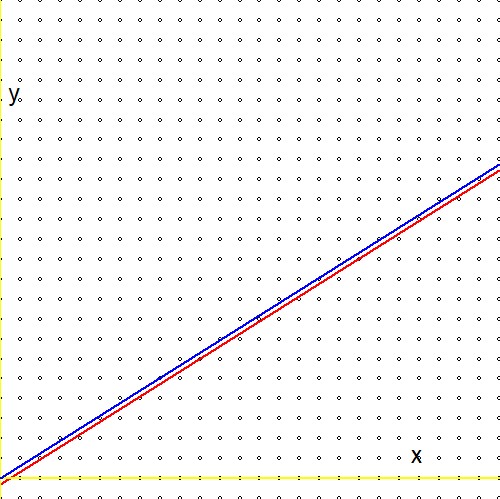
Do đó, CÂU HỎI: có tồn tại một phương tiện để điều chỉnh thủ tục Stern-Brocot sao cho nó hoạt động với các thực khác không?
BIÊN TẬP.
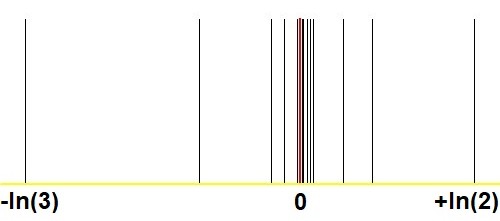
Đây là một biểu đồ khác cho thấy sự hội tụ đáng kinh ngạc với phương pháp Stern-Brocot, so với các hình ảnh tương tự trong phần Hỏi & Đáp của tôi Có thể gần đúng bất kỳ số thực dương nào bằng$2^m/3^n$ với $(m,n)$đủ lớn? :
Trả lời
Tôi sẽ đưa ra một cách tiếp cận không sử dụng quy trình Stern-Brocot.
Nó đủ để cho thấy rằng $\frac{2^{m}}{3^{n}}$dày đặc trong khoảng [1,2]. Kể từ khi lấy$\alpha\in (0,\infty)$ bên ngoài khoảng thời gian này có một số $k\in Z$ vậy nên $\alpha = 2^{k}\gamma $ cho một số $\gamma \in [1,2]$. Sau đó, chúng tôi biết có một trình tự trong$\frac{2^{m}}{3^{n}}$ cách tiếp cận nào $\gamma$, nhân dãy số theo thứ tự với $2^{k}$ (có thể lấy một phần đuôi của chuỗi), chúng tôi nhận được một chuỗi trong $\frac{2^{m}}{3^{n}}$ cách tiếp cận nào $\alpha$.
Tiếp theo hãy xem xét rằng bản đồ $f:[1,2] -> [0,1]$ với $f(x) = log_{2}(x)$ là một từ chối.
Hình ảnh của $\frac{2^{m}}{3^{n}}$ dưới bản đồ là $N-Nlog_{2}(3)$. Vì vậy, đủ để cho thấy rằng$N-Nlog_{2}(3)$ dày đặc trong $[0,1]$.
Đây là hệ quả của định lý Weyl's Equidistribution, là một trường hợp đặc biệt của định lý Ergodic.
Xem xét $a=2-log_{2}(3) = log_{2}(\frac{4}{3})$, vì thế $a$ là trong hình ảnh của bộ, $na = log_{2}(\frac{4^{n}}{3^{n}})$ và phần phân số của $na$.
Định lý Weyl Equidistribution (không phải là một kết quả tầm thường) cho thấy rằng đối với số vô tỷ, phần phân số của $na$được phân bố đồng đều và do đó dày đặc trên [0,1]. Từ$2-log_{2}(3)$ là không hợp lý, bạn có thể sử dụng định lý này.