Bằng vật lý Fermion

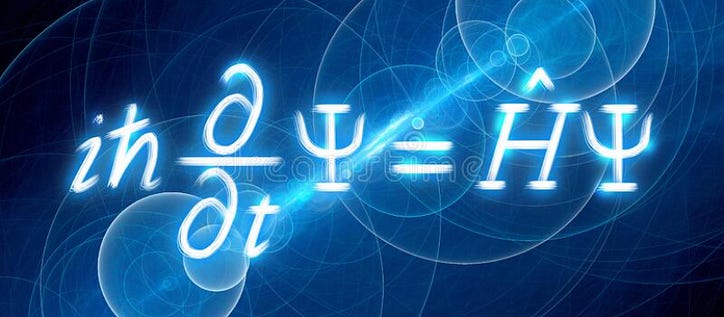
Nếu bạn đã học về vật lý lượng tử, hoặc ít nhất đã nghe nói về nó, bạn có thể đã nghe nói về anh chàng Schrodinger này. Bạn biết đấy - cái có toàn bộ con mèo? Chà, anh ấy cũng là người đứng sau một trong những phương trình hữu ích nhất trong cơ học lượng tử - phương trình Schrodinger. Thoạt nhìn, phương trình có vẻ không thể giải được (và thực tế là trong một số trường hợp, đúng là như vậy!), nhưng sau khi đọc phần này, bạn sẽ hiểu phương trình và thậm chí cả cách giải nó cho một tình huống. Sẳn sàng? Đi nào.

Đây là phương trình. Nó có vẻ đáng sợ — nó thậm chí còn có cả những cái chĩa ba trong đó! Nhưng chúng ta hãy cố gắng đạt được một số trực giác về phương trình này. Đầu tiên chúng ta sẽ bắt đầu bằng cách nói về năng lượng trong cơ học lượng tử, quảng bá chúng cho các toán tử, sau đó nói về vai trò của hàm sóng. Sau đó, chúng ta sẽ ghép mọi thứ lại với nhau và giải phương trình.

Cơ học cổ điển

Trong cơ học cổ điển (và cơ học lượng tử), công thức của năng lượng là E = KE + PE trong đó E là năng lượng toàn phần, KE là động năng và PE là thế năng. Bây giờ KE và PE hơi dài để viết, vì vậy để tiết kiệm vài mili giây viết, các nhà vật lý sử dụng các ký hiệu rõ ràng của T và V để biểu thị động năng và thế năng tương ứng. Vì vậy, bây giờ chúng ta có E = T + V

Chú thích cuối trang: Nếu bạn đã học về cơ học cổ điển, bạn có thể nhận thấy rằng chúng tôi đang sử dụng công thức Hamilton! Chúng ta sẽ giải quyết công thức Lagrange vào một ngày khác.

Bây giờ chúng ta biết rằng T=p²/2m (công thức cho động năng). Ở đây, m=khối lượng, p=động lượng, và ký hiệu khó nhất trong tất cả, ½=một nửa. Khối lượng luôn không đổi, nhưng động lượng không nhất thiết phải như vậy. Nếu ai đó tác dụng lực lên một vật, động lượng sẽ bắt đầu thay đổi và lệch khỏi giá trị ban đầu. Bây giờ những gì về năng lượng tiềm năng?

Công thức của thế năng là V= -(tích phân của F) trong đó F là lực. Rõ ràng là thế năng phụ thuộc vào lực tác dụng lên vật. Trong các tình huống khác nhau, năng lượng tiềm năng của bạn có thể mang các giá trị khác nhau do có các lực khác nhau. Ví dụ, trong giếng hấp dẫn, thế năng là V=mgx, nhưng trong máy dao động điều hòa, thế năng trở thành V=(1/2)kx². Điều này rất quan trọng vì hóa ra các “kịch bản” mà chúng ta giải phương trình Schrodinger thực sự chỉ là những thế năng khác nhau. Điều này sẽ có ý nghĩa sau này.

Lượng tử hóa đầu tiên

Bây giờ trong cơ học lượng tử, chúng ta lấy “vật quan sát” (T và E) của mình và làm cho chúng có toán tửđối tác. Đối với mục đích của chúng ta, một toán tử chỉ là một hàm nhận một giá trị và đưa ra một giá trị khác. Vì vậy, T có một đối lượng toán tử động năng, thường được ký hiệu là T', và năng lượng nhận một đối lượng toán tử năng lượng, thường được ký hiệu là H. Thế năng được “cho” thay vì được giải quyết, vì vậy nó không có bất kỳ đối tác điều hành. Bây giờ toán tử động năng được định nghĩa là toán tử mà khi nó tác động lên hàm sóng, nó trả về động năng của hạt nhân với hàm sóng. Điều tương tự với toán tử Năng lượng. Toàn bộ điều này có vẻ hơi vô dụng và trừu tượng, nhưng tin tôi đi, không phải vậy đâu - chúng ta đang đến đó. Bây giờ hãy nhớ cách T=(1/2m)p²? Điều này ngụ ý rằng T' = (1/2m)p̂², trong đó p̂ là toán tử động lượng . Và giống như trước đây, p̂ ψ = p ψtrong đó p là động lượng của hạt (một lần nữa, một toán tử tác động lên một hàm và trả về hàm đó nhân với bất kỳ giá trị nào có liên quan đến toán tử đó). Bây giờ hóa ra toán tử động lượng là

p̂ = -ih(d/dx). Hãy coi nó như một điều đã cho ngay bây giờ. Điều này ngụ ý rằng

T' = -h²/2m (d²/dx²). Và vì E = T + V, nên H=(-h²/2m)(d²/dx²) + V. Sau đó, bây giờ chúng ta có thể nhân cả hai vế với hàm sóng để có được

H ψ = -h²/2m (d²ψ/dx²) + Vψ

Và hãy nhớ từ trước đó, H ψ = Eψ, vì vậy

E ψ = (-h²/2m)(d²ψ/dx²) + Vψ

Bây giờ hãy hít một hơi thật sâu. Chúng tôi đã tính toán rất nhiều và hy vọng bạn không bị lạc. Hóa ra là chúng ta vừa “rút ra” phương trình Schrodinger! Bây giờ trước khi nói về việc giải quyết nó, chúng ta cần nói về “hàm sóng” này thậm chí là gì.

Hàm sóng là gì?

Trong cơ học cổ điển, chúng ta sử dụng phương trình Hamilton cổ điển để giải các phương trình chuyển động của hạt. Các phương trình chuyển động chỉ là các phương trình cho vị trí của một hạt tại một thời điểm nhất định. Ví dụ, phương trình chuyển động của một hạt tự do là x(t)=vt + x0. Chúng ta có thể tìm vị trí của hạt trong bất kỳ thời điểm nào nếu chúng ta có vị trí ban đầu và vận tốc. Trong cơ học lượng tử, thay vào đó, chúng ta sử dụng phương trình Schrodinger để tìm một thứ gọi là “hàm sóng”. Bản thân hàm sóng không có ý nghĩa vật lý — nó không có nghĩa gì cả và nó không cho bạn biết bất cứ điều gì (trực tiếp). Điều có ý nghĩa là bình phương của hàm sóng cung cấp cho bạn mật độ xác suất. Mật độ xác suất chỉ là một hàm cho bạn biết khả năng bạn tìm thấy một hạt trong một phạm vi nào đó khi bạn đo nó. Vì vậy, sau đó chúng ta có thể nói rằng hàm sóng chỉ là “căn bậc hai” của mật độ xác suất. Bây giờ chúng ta cuối cùng đã có tất cả kiến ​​thức cơ bản để nói về phương trình Schrodinger là gì .

Như chúng ta có thể thấy từ phương trình trên, mọi thứ đều không đổi ngoại trừ thế năng V(x). Chúng ta lấy một thế năng cụ thể và giải phương trình cho trường hợp bạn có thế năng cụ thể đó. Điều này thật tuyệt vời, bởi vì không quan trọng hệ thống của bạn có ứng suất nào, hay nhiệt, điện tích, điện áp, bạn đặt tên cho nó - bạn không cần tính đến bất kỳ điều gì trong số đó. Tất cả những gì bạn cần biết chỉ là hàm thế năng và bạn có thể giải phương trình

(Nếu chúng ta muốn trở thành mô phạm ở đây, chúng ta có thể nói rằng “về mặt kỹ thuật”, chúng ta đang kết hợp tất cả những thứ đó vào bên trong tiềm năng của chính nó. Ngoài ra, tam giác lộn ngược là viết tắt của đạo hàm cấp hai)

Phép tính

(nếu bạn không thích giải tích có thể bỏ qua phần này)

Bây giờ, hãy giải phương trình Schrodinger cho một điện thế đơn giản trong đó V(x)=0 ở mọi nơi. Đây được gọi là hạt tự do, vì tổng lực tác dụng lên nó bằng không. Nó tự do khỏi mọi áp bức! Trong trường hợp cổ điển, phương trình chuyển động sẽ là x(t)=vt + x0 tạo thành một đường thẳng trên đồ thị không-thời gian. Hãy xem hàm sóng trông như thế nào đối với trường hợp lượng tử.

Vì V(x)=0 nên phương trình schrodinger trở thành

-h²/2m(d² ψ/dx²) = Eψ

Sau đó chúng ta có thể thực hiện một số sắp xếp lại và nhận được

d² ψ/dx² = -2mEψ/h²

Bây giờ chúng ta có thể thấy rằng tất cả các số hạng ở vế phải đều không đổi ngoại trừ ψ. Điều này là tốt bởi vì nó làm cho phương trình dễ giải quyết. Khi đó chúng ta có thể định nghĩa một hằng số k là sqrt(2mE/h), có nghĩa là bây giờ chúng ta có

d²ψ / dx² = -k²ψ

Sau đó, chúng tôi thêm cả hai vế của phương trình bằng số hạng bên tay phải

d²ψ/dx² + k²ψ = 0

Khi đó chúng ta giả sử rằng ψ(x) = exp(rx)

và từ đó chúng tôi nhận được

r=-k², r= +ik hoặc -ik

Điều này có nghĩa là ψ( x)=exp(ikx) hoặc

ψ( x)=exp(-ikx)

Vì phương trình là tuyến tính, nên chúng ta có thể chồng chất (tổ hợp tuyến tính) của cả hai phần để có nghiệm chung

ψ(x) = Aexp(ikx) + Bexp(-ikx)

và chúng tôi đã hoàn thành về mặt kỹ thuật. Bạn có thể tự hỏi làm thế nào chúng ta thậm chí có thể xác định các hằng số A và B. Chúng ta thường làm điều này bằng một thứ gọi là chuẩn hóa, nhưng đó là câu chuyện của một thời điểm khác. Nó chỉ ra rằng kịch bản này không thể được bình thường hóa. Đó là ngôn ngữ ưa thích cho hàm sóng không tiến tới 0 khi bạn tiến tới vô cực hoặc âm vô cực. Vậy những giá trị A và B nào tương ứng với trạng thái này? Chà, hóa ra đây thực sự không phải là một trạng thái có thể xảy ra vì bạn không thể chuẩn hóa nó. Ối!

Đừng lo lắng mặc dù! Nó chỉ ra rằng sự chồng chất của tất cả các hàm sóng khả dĩ có thể mang lại một trạng thái thực. Điều này mang lại rất nhiều điều thú vị của riêng nó — nhưng đó cũng là một câu chuyện cho lần sau.

Cảm ơn vì đã đọc! Trang web này thực hiện rất tệ trong việc định dạng các ký hiệu toán học, vì vậy một số văn bản toán học không hiển thị đẹp mắt. Nếu bạn muốn xem một video dẫn xuất của cùng một thứ, tôi đã tạo một video ở đây trên kênh Vật lý Fermion của mình về giải pháp (mặc dù tôi nói khá nhanh). Chuyển đổi giữa video và bài viết này sẽ giúp giải pháp rõ ràng hơn. Cho đến thời điểm tiếp theo!