
Có một câu nói nổi tiếng được gán cho huấn luyện viên NBA và cựu cầu thủ Jason Kidd: "Chúng tôi sẽ xoay chuyển đội bóng này 360 độ!"
Rất tiếc. Các giáo viên dạy Toán chắc hẳn đã tròn mắt nhìn cái đó.
Như bạn có thể đã biết, một vòng tròn được tạo thành chính xác 360 độ. Nếu Kidd thực hiện tốt lời hứa của mình, thì đội của anh ta sẽ ổn thỏa. Rắc rối là, đội sẽ không ngừng quay cho đến khi "đi hết vòng tròn" và kết thúc ngay trở lại nơi bắt đầu.
Không phải là một công thức để cải thiện. Điều Kidd đang tìm kiếm là xoay chuyển đội của mình 180 độ và biến họ thành người chiến thắng!
Bằng cấp, xác định
Trong bối cảnh này, độ là một đơn vị chúng ta có thể sử dụng để đo góc . Trên giấy, độ được biểu thị bằng ký hiệu độ, trông giống như sau: °
Vì vậy, thay vì viết " 18 độ", bạn có thể chỉ cần viết " 18 ° " .
Một trong những khái niệm quan trọng nhất trong lượng giác và hình học là góc vuông . Đây là góc được hình thành tại đó hai đường thẳng vuông góc cắt nhau.
Nó cũng đại diện cho một phần tư của vòng quay đầy đủ.
Giả sử bạn muốn biến một cái gì đó về mặt vật lý. Bất cứ điều gì. Bạn đã chọn một điểm trung tâm cố định và đang cố gắng di chuyển đối tượng đó xung quanh nó theo chuyển động tròn. Nếu bạn hoàn thành công việc và tạo thành một vòng tròn hoàn chỉnh, đó là một vòng quay đầy đủ. Nhưng nếu bạn dừng quá trình này trong 25% chặng đường, thì đó chỉ là một phần tư của vòng quay đầy đủ. Điều này mang lại cho bạn một góc vuông.
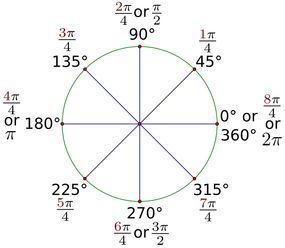
Một góc vuông bằng 90 độ (tức là 25 phần trăm của 360). Đây là một cách khác để đặt nó : Một góc vuông bằng π / 2 radian .
Hết giờ! Radian là gì? Và làm thế nào mà số π ( pi ) lại bị lẫn lộn trong điều này?
Mở gói Radian
OK, hãy tưởng tượng một vòng tròn hoàn hảo. Có một đường thẳng bắt đầu ở tâm chính xác của nó và kết thúc ở chu vi cong của hình tròn (như trong, cạnh ngoài).
Theo định nghĩa, đường thẳng đó là bán kính của đường tròn của chúng ta.
Về cơ bản, radian là một lát cắt của hình tròn. Nhìn vào chu vi cong bên ngoài của hình tròn một lần nữa. Bây giờ hãy tưởng tượng một đoạn của chu vi có độ dài bằng với bán kính của hình tròn của bạn. Nếu bạn vẽ hai đường thẳng nối hai điểm cuối của nó với tâm chính xác của vòng tròn, góc mà chúng tạo ra sẽ là một radian.
Mọi vòng tròn đều có chỗ cho cùng một số radian. Số đó bằng 2 lần số pi ("π"). Vì bản thân số pi bằng khoảng 3,14, bạn có thể nói có khoảng 6,28 radian trong một vòng tròn (2 x 3,14). Hoặc 1 radian đó là khoảng 57,29 độ (180 ° / π).
Radians Vs. Bằng cấp
Hãy nhìn xem, chúng tôi sẽ không phủ nhận nó. Radian có thể là một khái niệm khó hình dung hơn độ.
Nhưng đừng giảm giá trước. Cả hai đơn vị đo góc này đều có những ưu điểm của chúng.
Mức độ là cách phổ biến hơn. Trong thế giới thực, bạn có nhiều khả năng gặp phải những người nghĩ về độ trái ngược với radian. Vì vậy, nếu bạn đang cố gắng giao tiếp với một nhà không chuyên về toán học, có thể hãy chú ý đến mức độ.
Tuy nhiên, trong giải tích, radian rất tuyệt vời vì chúng cho phép các phương trình đơn giản hơn nhiều . Các học sinh AP trong tương lai sẽ muốn ghi nhớ điều đó.
Chuyển đổi độ sang Radian (và Vice Versa)
Để chuyển đổi độ sang radian, bạn chỉ cần ghi nhớ một vài bước đơn giản.
Đầu tiên, lấy số độ bạn muốn chuyển đổi. Nhân số này với π radian / 180 độ . Bằng cách loại bỏ một số đơn vị thừa và sau đó đơn giản hóa mọi thứ một chút, bạn sẽ có câu trả lời cho mình.
Giả sử bạn có một thanh kim loại được uốn một góc 120 độ. Làm thế nào chúng ta có thể diễn đạt điều này dưới dạng radian?
Để tìm hiểu, chúng tôi sẽ viết phương trình của chúng tôi như sau:
120 ° x (π radian / 180 ° )
Chú ý cặp ký hiệu độ được hiển thị ở trên. Chúng sẽ triệt tiêu lẫn nhau, đảm bảo câu trả lời cuối cùng của chúng tôi sẽ là radian. Bây giờ chúng tôi còn lại với:
120 x (π radian / 180)
Thực hiện phép nhân và bạn nhận được 120π / 180 radian . Nhưng chúng tôi vẫn chưa hoàn thành. Bây giờ chúng ta phải đơn giản hóa phân số của mình nếu có thể. Chúng ta cần xác định số nguyên cao nhất có thể chia chính xác cho cả mẫu số (180) và phần không phải là π của tử số (120). Cảnh báo spoiler: Trong trường hợp của chúng tôi, con số kỳ diệu là 60.
Nếu bạn thực sự chia 120π và 180 cho 60, bạn nhận được 2π / 3 radian.
Vì vậy, chúng ta đi: 120 ° bằng 2π / 3 radian.
Đi từ radian sang độ là một quy trình tương tự . Chỉ trong trường hợp này, chúng tôi sẽ lấy lượng radian ban đầu và nhân nó với (180 ° / π ).
π / 3 radian x (180 ° / π) = 60 độ
Tóm lại:
Để chuyển đổi từ radian sang độ : nhân với 180, chia cho π
Để chuyển đổi từ độ sang radian : nhân với π, chia cho 180
Bây giờ điều đó thật thú vị
Hình dạng "nhẫn", được tạo thành từ hai vòng tròn đồng tâm có chung tâm, về mặt kỹ thuật được gọi là "hình vòng cung ".















































